8. Algoritmi de programare dinamica
  8.1 Trei principii fundamentale ale programarii dinamice
  8.2 O competitie
  8.3 Inmultirea inlantuita a matricilor
  8.4 Tablouri multidimensionale
  8.5 Determinarea celor mai scurte drumuri intr-un graf
  8.6 Arbori binari optimi de cautare
  8.7 Arborii binari de cautare ca tip de data
    8.7.1 Arborele optim
    8.7.2 Cautarea in arbore
    8.7.3 Modificarea arborelui
  8.8 Programarea dinamica comparata cu tehnica greedy
  8.9 Exercitii

8. Algoritmi de programare dinamica

8.1 Trei principii fundamentale ale programarii dinamice

Programarea dinamica, ca si metoda divide et impera, rezolva problemele combinand solutiile subproblemelor. Dupa cum am vazut, algoritmii divide et impera partitioneaza problemele in subprobleme independente, rezolva subproblemele in mod recursiv, iar apoi combina solutiile lor pentru a rezolva problema initiala. Daca subproblemele contin subsubprobleme comune, in locul metodei divide et impera este mai avantajos de aplicat tehnica programarii dinamice.

Sa analizam insa pentru inceput ce se intampla cu un algoritm divide et impera in aceasta din urma situatie. Descompunerea recursiva a cazurilor in subcazuri ale aceleiasi probleme, care sunt apoi rezolvate in mod independent, poate duce uneori la calcularea de mai multe ori a aceluiasi subcaz, si deci, la o eficienta scazuta a algoritmului. Sa ne amintim, de exemplu, de algoritmul fib1 din Capitolul 1. Sau, sa calculam coeficientul binomial

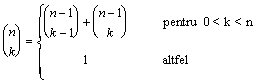
in mod direct:

function C(n, k)
     if k = 0 or k = n    then   return 1
                                 else   return C(n-1, k-1) + C(n-1, k)

Multe din valorile C(i, j), i < n, j < k, sunt calculate in mod repetat (vezi Exercitiul 2.5). Deoarece rezultatul final este obtinut prin adunarea a de 1, rezulta ca timpul de executie pentru un apel C(n, k) este in W( ).

Daca memoram rezultatele intermediare intr-un tablou de forma

(acesta este desigur triunghiul lui Pascal), obtinem un algoritm mai eficient. De fapt, este suficient sa memoram un vector de lungime k, reprezentand linia curenta din triunghiul lui Pascal, pe care sa-l reactualizam de la dreapta la stanga. Noul algoritm necesita un timp in O(nk). Pe aceasta idee se bazeaza si algoritmul fib2 (Capitolul 1). Am ajuns astfel la primul principiu de baza al programarii dinamice: evitarea calcularii de mai multe ori a aceluiasi subcaz, prin memorarea rezultatelor intermediare.

Putem spune ca metoda divide et impera opereaza de sus in jos (top-down), descompunand un caz in subcazuri din ce in ce mai mici, pe care le rezolva apoi separat. Al doilea principiu fundamental al programarii dinamice este faptul ca ea opereaza de jos in sus (bottom-up). Se porneste de obicei de la cele mai mici subcazuri. Combinand solutiile lor, se obtin solutii pentru subcazuri din ce in ce mai mari, pina se ajunge, in final, la solutia cazului initial.

Programarea dinamica este folosita de obicei in probleme de optimizare. In acest context, conform celui de-al treilea principiu fundamental, programarea dinamica este utilizata pentru a optimiza o problema care satisface principiul optimalitatii: intr-o secventa optima de decizii sau alegeri, fiecare subsecventa trebuie sa fie de asemenea optima. Cu toate ca pare evident, acest principiu nu este intotdeauna valabil si aceasta se intampla atunci cand subsecventele nu sunt independente, adica atunci cand optimizarea unei secvente intra in conflict cu optimizarea celorlalte subsecvente.

Pe langa programarea dinamica, o posibila metoda de rezolvare a unei probleme care satisface principiul optimalitatii este si tehnica greedy. In Sectiunea 8.1 vom ilustra comparativ aceste doua tehnici.

Ca si in cazul algoritmilor greedy, solutia optima nu este in mod necesar unica. Dezvoltarea unui algoritm de programare dinamica poate fi descrisa de urmatoarea succesiune de pasi:

·    se caracterizeaza structura unei solutii optime
·    se defineste recursiv valoarea unei solutii optime
·    se calculeaza de jos in sus valoarea unei solutii optime

Daca pe langa valoarea unei solutii optime se doreste si solutia propriu-zisa, atunci se mai efectueaza urmatorul pas:

·    din informatiile calculate se construieste de sus in jos o solutie optima

Acest pas se rezolva in mod natural printr-un algoritm recursiv, care efectueaza o parcurgere in sens invers a secventei optime de decizii calculate anterior prin algoritmul de programare dinamica.

8.2 O competitie

In acest prim exemplu de programare dinamica nu ne vom concentra pe principiul optimalitatii, ci pe structura de control si pe ordinea rezolvarii subcazurilor. Din aceasta cauza, problema considerata in aceasta sectiune nu va fi o problema de optimizare.

Sa ne imaginam o competitie in care doi jucatori A si B joaca o serie de cel mult 2n-1 partide, castigator fiind jucatorul care acumuleaza primul n victorii. Presupunem ca nu exista partide egale, ca rezultatele partidelor sunt independente intre ele si ca pentru orice partida exista o probabilitate p constanta ca sa castige jucatorul A si o probabilitate q = 1-p ca sa castige jucatorul B.

Ne propunem sa calculam P(i, j), probabilitatea ca jucatorul A sa castige competitia, dat fiind ca mai are nevoie de i victorii si ca jucatorul B mai are nevoie de j victorii pentru a castiga. In particular, la inceputul competitiei aceasta probabilitate este P(n, n), deoarece fiecare jucator are nevoie de n victorii. Pentru 1 £ i £ n, avem P(0, i) = 1 si P(i, 0) = 0. Probabilitatea P(0, 0) este nedefinita. Pentru i, j ³ 1, putem calcula P(i, j) dupa formula:

P(i, j) = pP(i-1, j) + qP(i, j-1)

algoritmul corespunzator fiind:

function P(i, j)
     if i = 0 then return 1
     if j = 0 then return 0
     return pP(i-1, j) + qP(i, j-1)

Fie t(k) timpul necesar, in cazul cel mai nefavorabil, pentru a calcula probabilitatea P(i, j), unde k = i+j.

Avem:

                        t(1) £ a

                        t(k) £ 2t(k-1) + c,    k > 1

a si c fiind doua constante. Prin metoda iteratiei, obtinem t Î O(2^k), iar daca i = j = n, atunci t Î O(4ⁿ). Daca urmarim modul in care sunt generate apelurile recursive (Figura 8.1), observam ca este identic cu cel pentru calculul ineficient al coeficientilor binomiali:

C(i+j, j) = C((i-1)+j, j) + C(i+( j-1), j-1)

Din Exercitiul 8.1 rezulta ca numarul total de apeluri recursive este

Timpul de executie pentru un apel P(n, n) este deci in W( ). Tinand cont si de Exercitiul 8.3, obtinem ca timpul pentru calculul lui P(n, n) este in O(4ⁿ) Ç W(4ⁿ/n). Aceasta inseamna ca, pentru valori mari ale lui n, algoritmul este ineficient.

Pentru a imbunatati algoritmul, vom proceda ca in cazul triunghiului lui Pascal. Tabloul in care memoram rezultatele intermediare nu il vom completa, insa, linie cu linie, ci pe diagonala. Probabilitatea P(n, n) poate fi calculata printr-un apel serie(n, p) al algoritmului

function serie(n, p)
     array P[0..n, 0..n]
     q ¬ 1-p
     for s ¬ 1 to n do
          P[0, s] ¬ 1; P[s, 0] ¬ 0
          for k ¬ 1 to s-1 do
              P[k, s-k] ¬ pP[k-1, s-k] + qP[k, s-k-1]
     for s ¬ 1 to n do
          for k ¬ 0 to n-s do
              P[s+k, n-k] ¬ pP[s+k-1, n-k] + qP[s+k, n-k-1]
     return P[n, n]

Deoarece in esenta se completeaza un tablou de n ´ n elemente, timpul de executie pentru un apel serie(n, p) este in Q(n²). Ca si in cazul coeficientilor binomiali, nu este nevoie sa memoram intregul tablou P. Este suficient sa memoram diagonala curenta din P, intr-un vector de n elemente.

8.3 Inmultirea inlantuita a matricilor

Ne propunem sa calculam produsul matricial

M = M₁ M₂ ... M_n

Deoarece inmultirea matricilor este asociativa, putem opera aceste inmultiri in mai multe moduri. Inainte de a considera un exemplu, sa observam ca inmultirea clasica a unei matrici de p ´ q elemente cu o matrice de q ´ r elemente necesita pqr inmultiri scalare.

Daca dorim sa obtinem produsul ABCD al matricilor A de 13 ´ 5, B de 5 ´ 89, C de 89 ´ 3 si D de 3 ´ 34 elemente, in functie de ordinea efectuarii inmultirilor matriciale (data prin paranteze), numarul total de inmultiri scalare poate sa fie foarte diferit:

(((AB)C)D)          10582   inmultiri
((AB)(CD))          54201   inmultiri
((A(BC))D)          2856     inmultiri
(A((BC)D))          4055     inmultiri
(A(B(CD)))          26418   inmultiri

Cea mai eficienta metoda este de aproape 19 ori mai rapida decat cea mai ineficienta. In concluzie, ordinea de efectuare a inmultirilor matriciale poate avea un impact dramatic asupra eficientei.

In general, vom spune ca un produs de matrici este complet parantezat, daca este: i) o singura matrice, sau ii) produsul a doua produse de matrici complet parantezate, inconjurat de paranteze. Pentru a afla in mod direct care este ordinea optima de efectuare a inmultirilor matriciale, ar trebui sa parantezam expresia lui M in toate modurile posibile si sa calculam de fiecare data care este numarul de inmultiri scalare necesare.

Sa notam cu T(n) numarul de moduri in care se poate paranteza complet un produs de n matrici. Sa presupunem ca decidem sa facem prima “taietura” intre a i-a si a (i+1)-a matrice a produsului

M = (M₁ M₂ ... M_i)(M_i+1 M_i+2 ... M_n)

Sunt acum T(i) moduri de a paranteza termenul stang si T(n-i) moduri de a paranteza termenul drept. Deoarece i poate lua orice valoare intre 1 si n-1, obtinem recurenta

cu T(1) = 1. De aici, putem calcula toate valorile lui T(n). De exemplu, T(5) = 14, T(10) = 4862, T(15) = 2674440. Valorile lui T(n) sunt cunoscute ca numerele catalane. Se poate demonstra ca

Din Exercitiul 8.3 rezulta T Î W(4ⁿ/n²). Deoarece, pentru fiecare mod de parantezare, operatia de numarare a inmultirilor scalare necesita un timp in W(n), determinarea modului optim de a-l calcula pe M este in W(4ⁿ/n). Aceasta metoda directa este deci foarte neperformanta si o vom imbunatati in cele ce urmeaza.

Din fericire, principiul optimalitatii se poate aplica la aceasta problema. De exemplu, daca cel mai bun mod de a inmulti toate matricile presupune prima taietura intre a i-a si a i+1-a matrice a produsului, atunci subprodusele M₁ M₂ ... M_i si M_i+1 M_i+2 ... M_n trebuie si ele calculate intr-un mod optim. Aceasta ne sugereaza sa aplicam programarea dinamica.

Vom construi tabloul m[1 .. n, 1 .. n], unde m[i, j] este numarul minim de inmultiri scalare necesare pentru a calcula partea M_i M_i+1 ... M_j a produsului initial. Solutia problemei initiale va fi data de m[1, n]. Presupunem ca tabloul d[0 .. n] contine dimensiunile matricilor M_i, astfel incat matricea M_i este de dimensiune d[i-1] ´ d[i], 1 £ i £ n. Construim tabloul m diagonala cu diagonala: diagonala s contine elementele m[i, j] pentru care j-i = s. Obtinem astfel succesiunea

s = 0         :  m[i, i] = 0,    i=1, 2, ..., n
s = 1         :  m[i, i+1] = d[i-1] d[i] d[i+1],    i=1, 2, ..., n-1

1 < s < n   :  m[i, i+s] =

(m[i, k] + m[k+1, i+s] + d[i-1] d[k] d[i+s]), i = 1, 2, ..., n-s

A treia situatie reprezinta faptul ca, pentru a calcula M_i M_i+1 ... M_i+s, incercam toate posibilitatile

(M_i M_i+1 ... M_k) (M_k+1 M_k+2 ... M_i+s)

si o alegem pe cea optima, pentru i £ k < i+s. A doua situatie este de fapt o particularizare a celei de-a treia situatii, cu s = 1.

Pentru matricile A, B, C, D, din exemplul precedent, avem

d = (13, 5, 89, 3, 34)

Pentru s = 1, gasim m[1, 2] = 5785, m[2, 3] = 1335, m[3, 4] = 9078. Pentru s = 2, obtinem

m[1, 3]  = min(m[1, 1] + m[2, 3] + 13´5´3, m[1, 2] + m[3, 3] + 13´89´3)

            = min(1530, 9256) = 1530

m[2, 4]  = min(m[2, 2] + m[3, 4] + 5´89´34, m[2, 3] + m[4, 4] + 5´3´34)

            = min(24208, 1845) = 1845

Pentru s = 3,

m[1, 4]  = min(  {k = 1}  m[1, 1] + m[2, 4] + 13´5´34,

                        {k = 2}  m[1, 2] + m[3, 4] + 13´89´34,

                        {k = 3}  m[1, 3] + m[4, 4] + 13´3´34)

            = min(4055, 54201, 2856) = 2856

Tabloul m este dat in Figura 8.2.

Sa calculam acum eficienta acestei metode. Pentru s > 0, sunt n-s elemente de calculat pe diagonala s; pentru fiecare, trebuie sa alegem intre s posibilitati (diferite valori posibile ale lui k). Timpul de executie este atunci in ordinul exact al lui

Timpul de executie este deci in Q(n³), ceea ce reprezinta un progres remarcabil fata de metoda exponentiala care verifica toate parantezarile posibile[*] .

Prin aceasta metoda, il putem afla pe m[1, n]. Pentru a determina si cum sa calculam produsul M in cel mai eficient mod, vom mai construi un tablou r[1 .. n, 1 .. n], astfel incat r[i, j] sa contina valoarea lui k pentru care este obtinuta valoarea minima a lui m[i, j]. Urmatorul algoritm construieste tablourile globale m si r.

procedure minscal(d[0 .. n])
     for i ¬ 1 to n do m[i, i] ¬ 0
     for s ¬ 1 to n-1 do
          for i ¬ 1 to n-s do
              m[i, i+s] ¬ +¥
              for k ¬ i to i+s-1 do
                   q ¬ m[i, k] + m[k+1, i+s] + d[i-1] d[k] d[i+s]
                   if q < m[i, i+s] then   m[i, i+s] ¬ q
                                                    r[i, i+s] ¬ k

Produsul M poate fi obtinut printr-un apel minmat(1, n) al algoritmului recursiv

function minmat(i, j)
     {returneaza produsul matricial M_i M_i+1 ... M_j
       calculat prin m[i, j] inmultiri scalare;
       se presupune ca i £ r[i, j] £ j}
     if i = j then return M_i
     arrays U, V
     U ¬ minmat(i, r[i, j])
     V ¬ minmat(r[i, j]+1, j)
     return produs(U, V)

unde functia produs(U, V) calculeaza in mod clasic produsul matricilor U si V. In exemplul nostru, produsul ABCD se va calcula in mod optim cu 2856 inmultiri scalare, corespunzator parantezarii: ((A(BC))D).

8.4 Tablouri multidimensionale

Implementarea operatiilor cu matrici si, in particular, a algoritmilor de inmultire prezentati in Sectiunile 7.8 si 8.3 necesita, in primul rand, clarificarea unor aspecte legate de utilizarea tablourilor in limbajele C si C++.

In privinta tablourilor, limbajul C++ nu aduce nimic nou fata de urmatoarele doua reguli preluate din limbajul C:

·    Din punct de vedere sintactic, notiunea de tablou multidimensional nu exista. Regula este surprinzatoare deoarece, in mod cert, putem utiliza tablouri multidimensionale. De exemplu, int a[2][5] este un tablou multidimensional (bidimensional) corect definit, avand doua linii si cinci coloane, iar a[1][2] este unul din elementele sale, si anume al treilea de pe a doua linie. Aceasta contradictie aparenta este generata de o ambiguitate de limbaj: prin int a[2][5] am definit, de fapt, doua tablouri de cate cinci elemente. Altfel spus, a este un tablou de tablouri si, ca o prima consecinta, rezulta ca numarul dimensiunilor unui “tablou multidimensional” este nelimitat. O alta consecinta este chiar modalitatea de memorare a elementelor. Asa cum este normal, cele doua tablouri (de cate cinci elemente) din a sunt memorate intr-o zona continua de memorie, unul dupa altul. Deci, elementele tablourilor bidimensionale sunt memorate pe linii. In general, elementele tablourilor multidimensionale sunt memorate astfel incat ultimul indice variaza cel mai rapid.
·    Un identificator de tablou este, in acelasi timp, un pointer a carui valoare este adresa primului element al tabloului. Prin aceasta regula, tablourile sunt identificate cu adresele primelor lor elemente. De exemplu, identificatorul a de mai sus (definit ca int a[2][5]) este de tip pointer la un tablou cu cinci elemente intregi, adica int (*)[5], iar a[0] si a[1] sunt adrese de intregi, adica int*. Mai exact, expresia a[0] este adresa primei linii din matrice (a primului tablou de cinci elemente) si este echivalenta cu *(a+0), iar expresia a[1] este adresa celei de-a doua linii din matrice (a celui de-al doilea tablou de cinci elemente), adica *(a+1). In final, deducem ca a[1][2] este echivalent cu *(*(a+1)+2), ceea ce ilustreaza echivalenta operatorului de indexare si a celui de indirectare.

In privinta echivalentei identificatorilor de tablouri si a pointerilor, nu mai putem fi atat de categorici. Sa pornim de la urmatoarele doua definitii:

int a[ 2 ][ 5 ];
int *b[ 2 ] = {
                a[ 0 ]    // adica b[ 0 ] = &a[ 0 ][ 0 ]
                a[ 1 ]    // adica b[ 1 ] = &a[ 1 ][ 0 ]
              };

unde a este un tablou de 2 ´ 5 elemente intregi, iar b este un tablou de doua adrese de intregi. Structura zonelor de memorie de la adresele a si b este prezentata in Figura 8.3.

Evaluand expresia b[1][2], obtinem *(*(b+1)+2), adica elementul a[1][2], element adresat si prin expresia echivalenta *(*(a+1)+2). Se observa ca valoarea pointerului *(b+1) este memorata in al doilea element din b (de adresa b+1), in timp ce valoarea *(a+1), tot de tip pointer la int, nu este memorata, fiind substituita direct cu adresa celei de-a doua linii din a. Pentru sceptici, programul urmator ilustreaza aceste afirmatii.

#include <iostream.h>

main( ) {
  int a[ 2 ][ 5 ];
  int *b[ 2 ] = { a[ 0 ], a[ 1 ] };

  cout << ( a + 1 ) << ' ' << *( a + 1 ) << '\n';
  cout << ( b + 1 ) << ' ' << *( b + 1 ) << '\n';

  return 1;
}

Tratarea diferita a expresiilor echivalente *(b+1) si *(a+1) se datoreaza faptului ca identificatorii de tablouri nu sunt de tip pointer, ci de tip pointer constant. Valoarea lor nu poate fi modificata, deoarece este o constanta rezultata in urma compilarii programului. Astfel, daca definim

char x[ ] = "algoritm";
char *y   = "eficient";

atunci x este adresa unei zone de memorie care contine textul “algoritm”, iar y este adresa unei zone de memorie care contine adresa sirului “eficient”.

Expresiile x[1], *(x+1) si expresiile y[1], *(y+1) sunt corecte, valoarea lor fiind al doilea caracter din sirurile “algoritm” si, respectiv, “eficient”. In schimb, dintre cele doua expresii *(++x) si *(++y), doar a doua este corecta, deoarece valoarea lui x nu poate fi modificata.

Prin introducerea claselor si prin posibilitatea de supraincarcare a operatorului [], echivalenta dintre operatorul de indirectare * si cel de indexare [] nu mai este valabila. Pe baza definitiei

int D = 8192;
// ...
tablou<int> x( D );

putem scrie oricand

for ( int i = 0; i < D; i++ ) x[ i ] = i;

dar nu si

for ( i = 0; i < D; i++ ) *( x + i ) = i;

deoarece expresia x+i nu poate fi calculata. Cu alte cuvinte, identificatorii de tip tablou<T> nu mai sunt asimilati tipului pointer. Intr-adevar, identificatorul x, definit ca tablou<float> x( D ), nu este identificatorul unui tablou predefinit, ci al unui tip definit utilizator, tip care, intamplator, are un comportament de tablou. Daca totusi dorim ca expresia *(x+i) sa fie echivalenta  cu x[i], nu avem decat sa definim in clasa tablou<T> operatorul

template <class T>
T* operator +( tablou<T>& t, int i ) {
  return &t[ i ];
}

In continuare, ne intrebam daca avem posibilitatea de a defini tablouri multidimensionale prin clasa tablou<T>, fara a introduce un tip nou. Raspunsul este afirmativ si avem doua variante de implementare:

·    Orice clasa permite definirea unor tablouri de obiecte. In particular, pentru clasa tablou<T>, putem s crie

tablou<int> c[ 3 ];

ceea ce inseamna ca c este un tablou de trei elemente de tip tablou<int>. Initializarea acestor elemente se realizeaza prin specificarea explicita a argumentelor constructorilor.

tablou<int> x( 5 );  // un tablou de 5 de elmente
tablou<int> c[ 3 ] = { tablou<int>( x ),
                       tablou<int>( 9 )
                     };

In acest exemplu, primul element se initializeaza prin constructorul de copiere, al doilea prin constructorul cu un singur argument int (numarul elementelor), iar al treilea prin constructorul implicit. In expresia c[1][4], care se refera la al cincilea element din cea de-a doua linie, primul operator de indexare folosit este cel predefinit, iar al doilea este cel supraincarcat in clasa tablou<T>. Din pacate, c este in cele din urma tot un tablou predefinit, avand deci toate deficientele mentionate in Sectiunea 4.1. In particular, este imposibil de verificat corectitudinea primului indice, in timp ce verificarea celui de-al doilea poate fi activata selectiv, pentru fiecare linie.

·    O a doua modalitate de implementare a tablourilor multidimensionale utilizeaza din plin facilitatile claselor parametrice. Prin instructiunea

tablou< tablou<int> > d( 3 );

obiectul d este definit ca un tablou cu trei elemente, fiecare element fiind un tablou de int.

Problema care apare aici este cum sa dimensionam cele trei tablouri membre, tablouri initializate prin constructorul implicit. Nu avem nici o modalitate de a specifica argumentele constructorilor (ca si in cazul alocarii tablourilor prin operatorul new), unica posibilitate ramanand atribuirea explicita sau functia de modificare a dimensiunii (redimensionare).

tablou<int> x( 25 );
tablou< tablou<int> > d( 3 );
d[ 0 ] = x;           // prima linie se initializeaza cu x
d[ 1 ].newsize( 16 ); // a doua linie se redimensioneaza
                      // a treia linie nu se modifica

Adresarea elementelor tabloului d consta in evaluarea expresiilor de genul d[1][4], unde operatorii de indexare [] sunt, de aceasta data, ambii din clasa parametrica tablou<T>. In consecinta, activarea verificarilor de indici poate fi invocata fie prin d.vOn(), pentru indicele de linie, fie separat in fiecare linie, prin d[i].vOn(),  pentru cel de coloana.

In anumite situatii, tablourile multidimensionale definite prin clasa parametrica tablou<T> au un avantaj important fata de cele predefinite, in ceea ce priveste consumul de memorie. Pentru fixarea ideilor, sa consideram tablouri bidimensionale, adica matrici. Daca liniile unei matrici nu au acelasi numar de elemente, atunci:

·    In tablourile predefinite, fiecare linie este de lungime maxima.
·    In tablourile bazate pe clasa tablou<T>, fiecare linie poate fi dimensionata corespunzator numarului efectiv de elemente.

O matrice este triunghiulara, atunci cand doar elementele situate de-o parte a diagonalei principale[**] sunt efectiv utilizate. In particular, o matrice triunghiulara este inferior triunghiulara, daca foloseste numai elementele de sub diagonala principala si superior trunghiulara, in caz contrar. Matricile trunghiulare au deci nevoie numai de aproximativ jumatate din spatiul necesar unei matrici obisnuite.

Tablourile bazate pe clasa tablou<T> permit implementarea matricilor triunghiulare in spatiul strict necesar, prin dimensionarea corespunzatoare a fiecarei linii. Pentru tablourile predefinite, acest lucru este posibil doar prin utilizarea unor artificii de calcul la adresarea elementelor.

8.5 Determinarea celor mai scurte drumuri intr-un graf

Fie G = <V, M> un graf orientat, unde V este multimea varfurilor si M este multimea muchiilor. Fiecarei muchii i se asociaza o lungime nenegativa. Dorim sa calculam lungimea celui mai scurt drum intre fiecare pereche de varfuri.

Vom presupune ca varfurile sunt numerotate de la 1 la n si ca matricea L da lungimea fiecarei muchii: L[i, i] = 0, L[i, j] ³ 0 pentru i ¹ j, L[i, j] = +¥ daca muchia (i, j) nu exista.

Principiul optimalitatii este valabil: daca cel mai scurt drum de la i la j trece prin varful k, atunci portiunea de drum de la i la k, cat si cea de la k la j, trebuie sa fie, de asemenea, optime.

Construim o matrice D care sa contina lungimea celui mai scurt drum intre fiecare pereche de varfuri. Algoritmul de programare dinamica initializeaza pe D cu L. Apoi, efectueaza n iteratii. Dupa iteratia k, D va contine lungimile celor mai scurte drumuri care folosesc ca varfuri intermediare doar varfurile din {1, 2, ..., k}. Dupa n iteratii, obtinem rezultatul final. La iteratia k, algoritmul trebuie sa verifice, pentru fiecare pereche de varfuri (i, j), daca exista sau nu un drum, trecand prin varful k, care este mai bun decat actualul drum optim ce trece doar prin varfurile din {1, 2, ..., k-1}. Fie D_k matricea D dupa iteratia k. Verificarea necesara este atunci:

D_k[i, j] = min(D_k-1[i, j], D_k-1[i, k] + D_k-1[k, j])

unde am facut uz de principiul optimalitatii pentru a calcula lungimea celui mai scurt drum via k. Implicit, am considerat ca un drum optim care trece prin k nu poate trece de doua ori prin k.

Acest algoritm simplu este datorat lui Floyd (1962):

function Floyd(L[1 .. n, 1 .. n])
     array D[1 .. n, 1 .. n]
     D ¬ L
     for k ¬ 1 to n do
          for i ¬ 1 to n do
              for j ¬ 1 to n do
                   D[i, j] ¬ min(D[i, j], D[i, k]+D[k, j])
     return D

De exemplu, daca avem

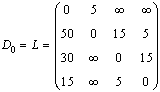
obtinem succesiv

Puteti deduce ca algoritmul lui Floyd necesita un timp in Q(n³). Un alt mod de a rezolva aceasta problema este sa aplicam algoritmul Dijkstra (Capitolul 6) de n ori, alegand mereu un alt varf sursa. Se obtine un timp in n Q(n²), adica tot in Q(n³). Algoritmul lui Floyd, datorita simplitatii lui, are insa constanta multiplicativa mai mica, fiind probabil mai rapid in practica. Daca folosim algoritmul Dijkstra-modificat in mod similar, obtinem un timp total in O(max(mn, n²) log n), unde m = #M. Daca graful este rar, atunci este preferabil sa aplicam algoritmul Dijkstra-modificat de n ori; daca graful este dens (m @ n²), este mai bine sa folosim algoritmul lui Floyd.

De obicei, dorim sa aflam nu numai lungimea celui mai scurt drum, dar si traseul sau. In acesta situatie, vom construi o a doua matrice P, initializata cu zero. Bucla cea mai interioara a algoritmului devine

if D[i, k]+D[k, j] < D[i, j]  then    D[i, j] ¬ D[i, k]+D[k, j]
                                                    P[i, j] ¬ k

Cand algoritmul se opreste, P[i, j] va contine varful din ultima iteratie care a cauzat o modificare in D[i, j]. Pentru a afla prin ce varfuri trece cel mai scurt drum de la i la j, consultam elementul P[i, j]. Daca P[i, j] = 0, atunci cel mai scurt drum este chiar muchia (i, j). Daca P[i, j] = k, atunci cel mai scurt drum de la i la j trece prin k si urmeaza sa consultam recursiv elementele P[i, k] si P[k, j] pentru a gasi si celelalte varfuri intermediare.

Pentru exemplul precedent se obtine

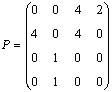
Deoarece P[1, 3] = 4, cel mai scurt drum de la 1 la 3 trece prin 4. Deoarece P[1, 4] = 2, cel mai scurt drum de la 1 la 4 trece prin 2. Rezulta ca cel mai scurt drum de la 1 la 3 este: 1, 2, 4, 3.

8.6 Arbori binari optimi de cautare

Un arbore binar in care fiecare varf contine o valoare (numita cheie) este un arbore de cautare, daca cheia fiecarui varf neterminal este mai mare sau egala cu cheile descendentilor sai stangi si mai mica sau egala cu cheile descendentilor sai drepti. Daca cheile arborelui sunt distincte, aceste inegalitati sunt, in mod evident, stricte.

Figura 8.4 este un exemplu de arbore de cautare[***] , continand cheile A, B, C, ..., H. Varfurile pot contine si alte informatii (in afara de chei), la care sa avem acces prin intermediul cheilor.

Aceasta structura de date este utila, deoarece permite o cautare eficienta a valorilor in arbore (Exercitiul 8.10). De asemenea, este posibil sa actualizam un arbore de cautare (sa stergem un varf, sa modificam valoarea unui varf, sau sa adaugam un varf) intr-un mod eficient, fara sa distrugem proprietatea de arbore de cautare.

Cu o multime data de chei, se pot construi mai multi arbori de cautare (Figura 8.5).

Pentru a cauta o cheie X in arborele de cautare, X va fi comparata la inceput cu cheia radacinii arborelui. Daca X este mai mica decat cheia radacinii, atunci se continua cautarea in subarborele stang; daca X este egala cu cheia radacinii, atunci cautarea se incheie cu succes; daca X este mai mare decat cheia radacinii, atunci se continua cautarea in subarborele drept. Se continua apoi recursiv acest proces.

De exemplu, in arborele din Figura 8.4 putem gasi cheia E prin doua comparatii, in timp ce aceeasi cheie poate fi gasita in arborele din Figura 8.5 printr-o singura comparatie. Daca cheile A, B, C, ..., H au aceeasi probabilitate, atunci pentru a gasi o cheie oarecare sunt necesare in medie:

(2+3+1+3+2+4+3+4)/8 = 22/8 comparatii,   pentru arborele din Figura 8.4
(4+3+2+3+1+3+2+3)/8 = 21/8 comparatii,   pentru arborele din Figura 8.5

Cand cheile sunt echiprobabile, arborele de cautare care minimizeaza numarul mediu de comparatii necesare este arborele de cautare de inaltime minima (demonstrati acest lucru si gasiti o metoda pentru a construi arborele respectiv!).

Vom rezolva in continuare o problema mai generala. Sa presupunem ca avem cheile c₁ < c₂ < ... < c_n si ca, in tabloul p, p[i] este probabilitatea cu care este cautata cheia c_i, 1 £ i £ n. Pentru simplificare, vom considera ca sunt cautate doar cheile prezente in arbore, deci ca p[1]+p[2]+...+p[n] = 1. Ne propunem sa gasim arborele optim de cautare pentru cheile c₁, c₂, ..., c_n, adica arborele care minimizeaza numarul mediu de comparatii necesare pentru a gasi o cheie.

Problema este similara cu cea a gasirii arborelui cu lungimea externa ponderata minima (Sectiunea 6.3), cu deosebirea ca, de aceasta data, trebuie sa mentinem ordinea cheilor. Aceasta restrictie face ca problema gasirii arborelui optim de cautare sa fie foarte asemanatoare cu problema inmultirii inlantuite a matricilor. In esenta, se poate aplica acelasi algoritm.

Daca o cheie c_i se afla intr-un varf de adincime d_i, atunci sunt necesare d_i +1 comparatii pentru a o gasi. Pentru un arbore dat, numarul mediu de comparatii necesare este

Dorim sa gasim arborele pentru care acest numar este minim.

Vom rezolva aceasta problema prin metoda programarii dinamice. Prima decizie consta in a determina cheia c_k a radacinii. Sa observam ca este satisfacut principiul optimalitatii: daca avem un arbore optim pentru c₁, c₂, ..., c_n si cu cheia c_k in radacina, atunci subarborii sai stang si drept sunt arbori optimi pentru cheile c₁, c₂, ..., c_k-1, respectiv c_k+1, c_k+2, ..., c_n. Mai general, intr-un arbore optim continand cele n chei, un subarbore oarecare este la randul sau optim pentru o secventa de chei succesive c_i, c_i+1, ..., c_j, i £ j.

In tabloul C, sa notam cu C[i, j] numarul mediu de comparatii efectuate intr-un subarbore care este optim pentru cheile c_i, c_i+1 ,..., c_j, atunci cand se cauta o cheie X in arborele optim principal. Valoarea

m[i, j] = p[i] + p[i+1] + ... + p[ j]

este probabilitatea ca X sa se afle in secventa c_i, c_i+1, ..., c_j. Fie c_k cheia radacinii subarborelui considerat. Atunci, probabilitatea compararii lui X cu c_k este m[i, j], si avem:

C[i, j] = m[i, j] + C[i, k-1] + C[k+1, j]

Pentru a obtine schema de programare dinamica, ramine sa observam ca c_k (cheia radacinii subarborelui) este aleasa astfel incat

C[i, j] = m[i, j] +

(C[i, k-1]+C[k+1, j])                       (*)

In particular, C[i, i] = p[i] si C[i, i-1] = 0.

Daca dorim sa gasim arborele optim pentru cheile c₁ < c₂ < ... < c₅, cu probabilitatile

p[1] = 0,30        p[2] = 0,05        p[3] = 0,08
p[4] = 0,45        p[5] = 0,12

calculam pentru inceput matricea m:

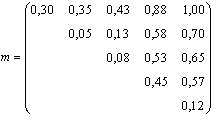
Sa notam ca C[i, i] = p[i], 1 £ i £ 5. Din relatia (*), calculam celelalte valori pentru C[i, j]:

C[1, 2]  = m[1, 2] + min(C[1, 0]+C[2, 2], C[1, 1]+C[3, 2])
            = 0,35 + min(0,05, 0,30) = 0,40

Similar,

C[2, 3] = 0,18               C[3, 4] = 0,61               C[4, 5] = 0,69

Apoi,

C[1, 3]  = m[1, 3] + min(C[1, 0]+C[2, 3], C[1, 1]+C[3, 3], C[1, 2]+C[4, 3])
            = 0,43 + min(0,18, 0,38, 0,40) = 0,61

C[2, 4] = 0,76               C[3, 5] = 0,85

C[1, 4] = 1,49               C[2, 5] = 1,00

C[1, 5] = m[1, 5] + min(C[1, 0]+C[2, 5], C[1, 1]+C[3, 5], C[1, 2]+C[4, 5],
                                     C[1, 3]+C[5, 5], C[1, 4]+C[6, 5]) = 1,73

Arborele optim necesita deci in medie 1,73 comparatii pentru a gasi o cheie.

In acest algoritm, calculam valorile C[i, j] in primul rand pentru j-i = 1, apoi pentru j-i = 2 etc. Cand j-i = q, avem de calculat n-q valori ale lui C[i, j], fiecare implicand o alegere intre q+1 posibilitati. Timpul necesar [****] este deci in

Stim acum cum sa calculam numarul minim de comparatii necesare pentru a gasi o cheie in arborele optim. Mai ramane sa construim efectiv arborele optim. In paralel cu tabloul C, vom construi tabloul r, astfel incat r[i, j] sa contina valoarea lui k pentru care este obtinuta in relatia (*) valoarea minima a lui C[i, j], unde i < j. Generam un arbore binar, conform urmatoarei metode recursive:

·    radacina este etichetata cu (1, n)
·    daca un varf este etichetat cu (i, j), i < j, atunci fiul sau stang va fi etichetat cu (i, r[i, j]-1) si fiul sau drept cu (r[i, j]+1, j)
·    varfurile terminale sunt etichetate cu (i, i)

Plecand de la acest arbore, arborele de cautare optim se obtine schimband etichetele (i, j), i < j, in c_r[i, j], iar etichetele (i, i) in c_i.

Pentru exemplul precedent, obtinem astfel arborele optim din Figura 8.6.

Problema se poate generaliza, acceptand sa cautam si chei care nu se afla in arbore. Arborele optim de cautare se obtine in mod similar.

8.7 Arborii binari de cautare ca tip de data

Intr-o prima aproximare, arborele binar este un tip de data similar tipului lista. Varfurile sunt compuse din informatie (cheie) si legaturi, iar arborele propiu-zis este complet precizat prin adresa varfului radacina. In privinta organizarii memoriei, putem opta fie pentru tablouri paralele, ca in Exercitiul 8.10, fie pentru alocarea dinamica a elementelor. Alegand alocarea dinamica, vom utiliza in intregime modelul oferit de clasa lista<E> elaborata in Sectiunea 4.3. Astfel, clasa parametrica arbore<E>, cu o structura interna de forma:

template <class E>
class arbore {
  // ... declaratii friend
public:
  arbore( )  { root = 0; n = 0; }

  // ... functii membre

private:
  varf<E> *root;  // adresa varfului radacina
  int      n;     // numarul varfurilor din arbore
};

are la baza o clasa privata varf<E> prin intermediul careia vom implementa majoritatea operatiilor efectuate asupra arborilor. Vom cauta sa izolam, ori de cate ori va fi posibil, operatiile direct aplicabile varfurilor, astfel incat interfata dintre cele doua clase sa fie foarte clar precizata printr-o serie de “operatii elementare”.

Nu vom implementa in aceasta sectiune arbori binari in toata generalitatea lor, ci doar arborii de cautare. Obiectivul urmarit in prezentarea listelor a fost structura de date in sine, impreuna cu procedurile generale de manipulare. In cazul arborelui de cautare, nu mai este necesara o astfel de generalitate, deoarece vom implementa direct operatiile specifice. In mare, aceste operatii pot fi impartite in trei categorii:

·    Cautari. Localizarea varfului cu o anumita cheie, a succesorului sau predecesorului lui, precum si a varfurilor cu cheile de valoare maxima, respectiv minima.
·    Modificari. Arborele se modifica prin inserarea sau stergerea unor varfuri.
·    Organizari. Arborele nu este construit prin inserarea elementelor, ci global, stabilind intr-o singura trecere legaturile dintre varfuri. Frecvent, organizarea se face conform unor criterii pentru optimizarea cautarilor. Un caz particular al acestei operatii este reorganizarea arborelui dupa o perioada suficient de mare de utilizare. Este vorba de reconstruirea arborelui intr-o structura optima, pe baza statisticilor de utilizare.

Datorita operatiilor de cautare si modificare, elementele de tip E trebuie sa fie comparabile prin operatorii uzuali ==, !=, >. In finalul Sectiunii 7.4.1, am aratat ca o asemenea pretentie nu este totdeauna justificata. Desigur ca, in cazul unor structuri bazate pe relatia de ordine, asa cum sunt heap-ul si arborele de cautare, este absolut normal ca elementele sa poata fi comparate.

Principalul punct de interes pentru noi este optimizarea, conform algoritmului de programare dinamica. Nu vom ignora nici cautarile, nici operatiile de modificare (tratate in Sectiunea 8.7.2).

8.7.1 Arborele optim

Vom rezolva problema obtinerii arborelui optim in cel mai simplu caz posibil (din punct de vedere al utilizarii, dar nu si in privinta programarii): arborele deja exista si trebuie reorganizat intr-un arbore de cautare optim. Avand in vedere specificul diferit al operatiilor de organizare fata de celelalte operatii efectuate asupra grafurilor, am considerat util sa incapsulam optimizarea intr-o clasa pe care o vom numi “structura pentru optimizarea arborilor” sau, pe scurt, s8a.

Clasa s8a este o clasa parametrica privata, asociata clasei arbore<E>. Functionalitatea ei consta in:

i)     initializarea unui tablou cu adresele varfurilor in ordinea crescatoare a probabilitatilor cheilor
ii)    stabilirea de noi legaturi intre varfuri astfel incat arborele sa fie optim.

Principalul motiv pentru care a fost aleasa aceasta implementare este ca sunt necesare doar operatii modificare a legaturilor. Deplasarea unui varf (de exemplu, pentru sortare) inseamna nu numai deplasarea cheii, ci si a informatiei asociate. Cum fiecare din aceste elemente pot fi oricat de mari, clasa s8a realizeaza o economie semnificativa de timp si (mai ales) de memorie.

Pentru optimizarea propriu-zisa, am implementat atat algoritmul de programare dinamica, cat si pe cel greedy prezentat in Exercitiul 8.12. Desi algoritmul greedy nu garanteaza obtinerea arborelui optim, el are totusi avantajul ca este mai eficient decat algoritmul de programare dinamica din punct de vedere al timpului de executie si al memoriei utilizate. Invocarea optimizarii se realizeaza din clasa arbore<E>, prin secvente de genul

arbore<float> af;

// arborele af se creeaza prin inserarea cheilor
// arborele af se utilizeaza

// pe baza probabilitatilor predefinite si actualizate
//  prin utilizarea arborelui se invoca optimizarea

af.re_prodin( ); // sau af.re_greedy( );

unde functiile membre re_greedy() si re_prodin() sunt definte astfel:

template <class E>
arbore<E>& arbore<E>::re_greedy( ) {
// reorganizare prin metoda greedy
  s8a<E> opt( root, n );
  root = opt.greedy( );
  return *this;
}

template <class E>
arbore<E>& arbore<E>::re_prodin( ) {
// reorganziare prin programare dinamica
  s8a<E> opt( root, n );
  root = opt.prodin( );
  return *this;
}

Dupa adaugarea tuturor functiilor si datelor membre necesare implementarii functiilor greedy() si prodin(), clasa s8a are urmatoarea structura:

template <class E>
class s8a {   // clasa pentru construirea arborelui optim
  friend class arbore<E>;
private:
  s8a( varf<E> *root, int nn ): pvarf( n = nn ) {
    int i = 0;          // indice in pvarf
    setvarf( i, root ); // setarea elementelor din pvarf
  }

  // initializarea tabloului pvarf cu un arbore deja format
  void setvarf( int&, varf<E>* );
  varf<E>* greedy( ) {  // "optim" prin algoritmul greedy
    return _greedy( 0, n );
  }

  varf<E>* prodin( ) {  // optim prin programare dinamica
    _progDinInit( ); return _progDin( 0, n - 1 );
  }

  // functiile prin care se formeaza efectiv arborele
  varf<E>* _greedy     ( int, int );
  varf<E>* _progDin    ( int, int );
  void     _progDinInit( );   // initializeaza tabloul r

  // date membre
  tablou<varf<E>*> pvarf;  // tabloul adreselor varfurilor
  int n;                   // numarul varfurilor din arbore

  // tabloul indicilor necesar alg. de programare dinamica
  tablou< tablou<int> > r;
};

In stabilirea valorilor tablourilor pvarf si r se pot distinge foarte clar cele doua etape ale executiei constructorului clasei s8a, etape mentionate in Sectiunea 4.2.1. Este vorba de etapa de initializare (implementata prin lista de initializare a membrilor) si de etapa de atribuire (implementata prin corpul constructorului). Lista de initializare asociata constructorului clasei s8a contine parametrul necesar dimensionarii tabloului pvarf pentru cele n elemente ale arborelui. Cum este insa initializat tabloul r care nu apare in lista de initializare? In astfel de cazuri, se invoca automat constructorul implicit (apelabil fara nici un argument) al clasei respective. Pentru clasa tablou<T>, constructorul implicit doar initializeaza cu 0 datele membre.

Etapa de atribuire a constructorului clasei s8a, implementata prin invocarea functiei setvarf(), consta in parcurgerea arborelui si memorarea adreselor varfurilor vizitate in tabloul pvarf. Functia setvarf() parcurge pentru fiecare varf subarborele stang, apoi memoreaza adresa varfului curent si, in final, parcurge subarborele drept. Dupa cum vom vedea in Exercitiul 9.1, acest mod de parcurgere are proprietatea ca elementele arborelui sunt parcurse in ordine crescatoare. De fapt, este vorba de o metoda de sortare similara quicksort-ului, varful radacina avand acelasi rol ca si elementul pivot din quicksort.

template <class E>
void s8a<E>::setvarf( int& poz, varf<E>* x ) {

  if ( x ) {
    setvarf( poz, x->st );
    pvarf[ poz++ ] = x;
    setvarf( poz, x->dr );

    // anulam toate legaturile elementului x
    x->st = x->dr = x->tata = 0;
  }
}

In aceasta functie, x->st, x->dr si x->tata sunt legaturile varfului curent x catre fiul stang, catre cel drept si, respectiv, catre varful tata. In plus fata de aceste legaturi, obiectele de tip varf<E> mai contin cheia (informatia) propriu-zisa si un camp auxiliar pentru probabilitatea varfului (elementului). In consecinta, clasa varf<E> are urmatoarea structura:

template <class E>
class varf {
  friend class arbore<E>;
  friend class s8a<E>;

private:
  varf( const E& v, float f = 0 ): key( v )
    { st = dr = tata = 0; p = f; }

  varf<E>   *st; // adresa fiului stang
  varf<E>   *dr; // adresa fiului drept
  varf<E> *tata; // adresa varfului tata

  E         key; // cheia
  float       p; // frecventa utilizarii cheii curente
};

Implementarea celor doua metode de optimizare a arborelui urmeaza pas cu pas algoritmul greedy si, respectiv, algoritmul de programare dinamica. Ambele (re)stabilesc legaturile dintre varfuri printr-un proces recursiv, pornind fie direct de la probabilitatile elementelor, fie de la o matrice (matricea r) construita pe baza acestor probabilitati. Functiile care stabilesc legaturile, adica _progDin() si _greedy(), sunt urmatoarele:

template <class E>
varf<E>* s8a<E>::_greedy( int m, int M ) {
  // m si M sunt limitele subsecventei curente
  if ( m == M ) return 0;

  // se determina pozitia k a celei mai frecvente chei
  int k;                  float pmax = pvarf[ k = m ]->p;
  for ( int i = m; ++i < M; )
    if ( pvarf[ i ]->p > pmax ) pmax = pvarf[ k = i ]->p;

  // se selecteaza adresa varfului de pe pozitia k
  varf<E> *actual = pvarf[ k ];

  // se construiesc subarborii din stanga si din deapta
  // se initializeaza legatura spre varful tata
  if ( (actual->st = _greedy( m,     k )) != 0 )
    actual->st->tata = actual;
  if ( (actual->dr = _greedy( k + 1, M )) != 0 )
    actual->dr->tata = actual;

  // subarborele curent este gata; se returneaza adresa lui
  return actual;
}

template <class E>
varf<E>* s8a<E>::_progDin( int i, int j ) {
  // i si j, i <=j, sunt coordonatele radacinii
  //  subarborelui curent in tabloul r
  if ( i > j ) return 0;

  // se selecteaza adresa varfului radacina
  varf<E> *actual = pvarf[ r[ j ][ i ] ];

  if ( i != j ) { // daca nu este un varf frunza ...
    // se construiesc subarborii din stanga si din deapta
    // se initializeaza legatura spre varful tata
    if ( (actual->st = _progDin( i, r[j][i] - 1 )) != 0 )
       actual->st->tata = actual;
    if ( (actual->dr = _progDin( r[j][i] + 1, j )) != 0 )
       actual->dr->tata = actual;
  }

  // subarborele curent este gata; se returneaza adresa lui
  return actual;
}

Folosind notatiile introduse in descrierea algoritmului de optimizare prin programare dinamica, functia _progDinInit() construieste matricea r, unde r[i][j], i < j, este indicele in tabloul pvarf al adresei varfului etichetat cu (i, j). In acest scop, se foloseste o alta matrice C, unde C[i][j], i < j, este numarul de comparatii efectuate in subarborele optim al cheilor cu indicii i, ..., j.  Initial, C este completata cu probabilitatile cumulate ale cheilor de indici i, ..., j.

Se observa ca matricile r si C sunt superior triunghiulare. Totusi, pentru implementare, am preferat sa lucram cu matrici inferior triunghiulare, adica cu transpusele matricilor r si C, deoarece adresarea elementelor ar fi fost altfel mai complicata.

template <class E>
void s8a<E>::_progDinInit( ) {
  int i, j, d;
 tablou< tablou<float> > C;   // tabloul C este local

  // redimensionarea si initializarea tablourilor C si r
  //  ATENTIE! tablourile C si r sunt TRANSPUSE.
  r.newsize( n );
  C.newsize( n );
  for ( i = 0; i < n; i++ ) {
    r[ i ].newsize( i + 1 ); r[ i ][ i ] = i;
    C[ i ].newsize( i + 1 ); C[ i ][ i ] = pvarf[ i ]->p;
  }

  // pentru inceput C este identic cu m
  for ( d = 1; d < n; d++ )
    for ( i = 0; (j = i + d) < n; i++ )
      C[ j ][ i ] = C[ j - 1 ][ i ] + C[ j ][ j ];

  // elementele din C se calculeaza pe diagonale
  for ( d = 1; d < n; d++ )
    for ( i = 0; (j = i + d) < n; i++ ) {
      // in calculul minimului dintre C[i][k-1]+C[k+1][j]
      //  consideram mai intai cazurile k=i si k=j in care
      //  avem C[i][i-1] = 0 si C[j+1][j] = 0
      int k; float Cmin;
      if ( C[ j ][ i + 1 ] < C[ j - 1 ][ i ] )
        Cmin = C[ j ][ (k = i) + 1 ];
      else
        Cmin = C[ (k = j) - 1 ][ i ];

      // au mai ramas de testat elementele i+1, ..., j-1
      for ( int l = i + 1; l < j; l++ )
        if ( C[ l - 1 ][ i ] + C[ j ][ l + 1 ] < Cmin )
          Cmin = C[ (k = l) - 1 ][ i ] + C[ j ][ l + 1 ];

      // minimul si pozitia lui sunt stabilite ...
      C[ j ][ i ] += Cmin;
      r[ j ][ i ] = k;
    }
}

8.7.2 Cautarea in arbore

Principala operatie efectuata prin intermediul arborilor binari de cautare este regasirea informatiei asociate unei anumite chei. Functia de cautare search() are ca argument cheia pe baza careia se va face cautarea si returneaza false sau true, dupa cum cheia fost regasita, sau nu a fost regasita in arbore. Cand cautarea s-a terminat cu succes, valoarea din arbore a cheii regasite este returnata prin intermediul argumentului de tip referinta, pentru a permite consultarea informatiilor asociate.

template <class E>
int arbore<E>::search( E& k ) {
  varf<E> *x = _search( root, k );
  if ( !x )   return 0; // element absent
  x->p++;               // actualizarea frecventei
  k = x->key; return 1;
}

Actualizarea probabilitatilor cheilor din arbore, dupa fiecare operatie de cautare, este ceva mai delicata, deoarece impune stabilirea importantei evaluarilor existente in raport cu rezultatele cautarilor. De fapt, este vorba de un proces de invatare care porneste de la anumite cunostinte deja acumulate. Problema este de a stabili gradul de importanta al cunostintelor existente in raport cu cele nou dobandite. Inainte de a prezenta o solutie elementara a acestei probleme, sa observam ca algoritmii de optimizare lucreaza cu probabilitati, dar numai ca ponderi. In consecinta, rezultatul optimizarii nu se schimba, daca in loc de probabilitati se folosesc frecvente absolute.

Fie trei chei ale caror probabilitati de cautare au fost estimate initial la 0,18, 0,65, 0,17. Sa presupunem ca se doreste optimizarea arborelui de cautare asociat acestor chei, atat pe baza acestor estimari, cat si folosind rezultatele a 1000 de cautari de instruire terminate cu succes[*****] . Daca fixam ponderea estimarilor initiale in raport cu rezultatele instruirii la 5 / 2, atunci vom initializa membrul p (estimarea probabilitatii cheii curente) din clasa varf<E> cu valorile

0,18 ´ 1000 ´  (5 / 2) = 450
0,65 ´ 1000 ´ (5 / 2)  = 1625
 0,17 ´ 1000 ´ (5 / 2)  = 425

Apoi, la fiecare cautare terminata cu success, membrul p corespunzator cheii gasite se incrementeaza cu 1. De exemplu, daca prima cheie a fost gasita in 247 cazuri, a doua in 412 cazuri si a treia in 341 cazuri, atunci valorile lui p folosite la optimizarea arborelui vor fi 697, 2037 si 766. Suma acestor valori este 3500, valoare care corespunde celor 1000 de incercari plus ponderea de 1000 ´  (5 / 2) = 2500 asociata estimarii initiale. Noile probabilitati, invatate prin instruire, sunt:

697 / 3500 @ 0,20
2037 / 3500 @ 0,58
766 / 3500 @ 0,22

Pentru verificarea rezultatelor de mai sus, sa refacem calculele, lucrand numai cu probabilitati. Estimarile initiale ale probabilitatilor sunt 0,18, 0,65 si 0,17. In urma instruirii, cele trei chei au fost cautate cu probabilitatile:

247 / 1000 = 0,247
412 / 1000 = 0,412
697 / 1000 = 0,697

Avand in vedere raportul de 5 / 2 stabilit intre estimarea initiala si rezultatele instruirii, probabilitatile finale[******] sunt:

(0,18 ´ 5 + 0,247 ´ 2) / 7 @ 0,20
(0,65 ´ 5 + 0,412 ´ 2) / 7 @ 0,58
(0,17 ´ 5 + 0,697 ´ 2) / 7 @ 0,22

Cautarea este, de fapt, o parcurgere a varfurilor, realizata prin functia _search(varf<E>*, const E&). Aceasta functie nu face parte din clasa arbore<E>, deoarece opereaza exclusiv asupra varfurilor. Iata varianta ei recursiva, impreuna cu alte doua functii asemanatoare: _min(), pentru determinarea varfului minim din arbore si _succ(), pentru determinarea succesorului[*******] .

template <class E>
varf<E>* _search( varf<E>* x, const E& k ) {
  while ( x != 0 && k != x->key )
    x = k > x->key? x->dr: x->st;
  return x;
}

template <class E>
varf<E>* _min( varf<E>* x ) {
  while ( x->st != 0 )
    x = x->st;
  return x;
}

template <class E>
varf<E>* _succ( varf<E>* x ) {
  if ( x->dr != 0 ) return _min( x->dr );

  varf<E> *y = x->tata;
  while ( y != 0 && x == y->dr )
    { x = y; y = y->tata; }
  return y;
}

Existenta acestor functii impune completarea clasei varf<E> cu declaratiile friend corespunzatoare.

Sa remarcam asemanarea dintre functiile C++ de mai sus si functiile analoage din Exercitiul 8.10.

Pentru a demonstra corectitudinea functiilor _serarch() si _min(), nu avem decat sa ne reamintim ca, prin definitie, intr-un arbore binar de cautare fiecare varf K verifica relatiile X £ K si K £ Y  pentru orice varf X din subarborele stang si orice varf Y din subarborele drept.

Demonstrarea corectitudinii functiei _succ() este de asemenea foarte simpla. Fie K varful al carui succesor S trebuie determinat. Varfurile K si S pot fi situate astfel:

·    Varful S este in subarborele drept al varfului K. Deoarece aici sunt numai varfuri Y cu proprietatea K £ Y (vezi Figura 8.7a) rezulta ca S este valoarea minima din acest subarbore. In plus, avand in vedere procedura pentru determinarea minimului, varful S nu are fiul stang.
·    Varful K este in subarborele stang al varfului S. Deoarece fiecare varf X de aici verifica inegalitatea X £ S  (vezi Figura 8.7b), deducem ca  maximul din acest subarbore este chiar K. Dar maximul se determina parcurgand fiii din dreapta pana la un varf fara fiul drept. Deci, varful K nu are fiul drept, iar S este primul ascendent din stanga al varfului K.

In consecinta, cele doua situatii se exclud reciproc, deci functia _succ() este corecta.

8.7.3 Modificarea arborelui

Modificarea structurii arborelui de cautare, prin inserarea sau stergerea unor varfuri trebuie realizata astfel incat proprietatea de arbore de cautare sa nu se altereze. Cele doua operatii sunt diferite in privinta complexitatii. Inserarea este simpla, fiind similara cautarii. Stergerea este mai dificila si mult diferita de operatiile cu care deja ne-am obisnuit.

Pentru inserarea unei noi chei, vom folosi functia

template <class E>
int arbore<E>::ins( const E& k, float p ) {
  varf<E> *y = 0, *x = root;

  while ( x != 0 ) {
    y = x;
    if ( k == x->key ) { // cheia deja exista in arbore
      x->p += p;         // se actualizeaza frecventa
      return 0;          // se returneaza cod de eroare
    }
    x = k > x->key? x->dr: x->st;
  }

  // cheia nu exista in arbore
  varf<E> *z = new varf<E>( k, p );
  z->tata = y;

  if ( y == 0 )                  root = z;
  else   if ( z->key > y->key ) y->dr = z;
         else                   y->st = z;

  n++;   // in arbore este cu un varf mai mult
  return 1;
}

Valoarea returnata este true, daca cheia k a putut fi inserata in arbore, sau false, in cazul in care deja exista in arbore un varf cu cheia k. Inserarea propriu-zisa consta in cautarea cheii k prin intermediul adreselor x si y, y fiind adresa tatalui lui x. Atunci cand am terminat procesul de cautare, valoarea lui x devine 0 si noul varf se va insera la stanga sau la dreapta lui y, in functie de relatia dintre cheia k si cheia lui y.

Procedura de stergere incepe prin a determina adresa z a varfului de sters, pe baza cheii k. Daca procesul de cautare se finalizeaza cu succes, cheia k se va actualiza (in scopul unor prelucrari ulterioare) cu informatia din varful z, iar apoi se demareaza procesul de stergere efectiva a varfului z. Daca z este un varf terminal, nu avem decat sa anulam legatura corespunzatoare din varful tata. Chiar si atunci cand z are un singur fiu, stergerea este directa. Adresa lui z din varful tata se inlocuieste cu adresa fiului lui z. A treia si cea mai complicata situatie apare atunci cand z este situat undeva in interiorul arborelui, avand ambele legaturi complete. In acest caz, nu vom mai sterge varful z, ci varful y, succesorul lui z, dar nu inainte de a copia continutul lui y in z. Stergerea varfului y se face conform unuia din cele doua cazuri de mai sus, deoarece, in mod sigur, y nu are fiul stang. Intr-adevar, intr-un arbore de cautare, succesorul unui varf cu doi fii nu are fiul stang, iar predecesorul[********] unui varf cu doi fii nu are fiul drept (demonstrati acest lucru!). Pentru ilustrarea celor trei situatii, am sters din arborele din Figura 8.8a varfurile E (varf cu doi fii), A (varf cu un fiu) si L (varf terminal).

Procedura de stergere se implementeaza astfel:

template <class E>
int arbore<E>::del( E& k ) {
  varf<E> *z = _search( root, k );  // se cauta cheia k
  if ( !z ) return 0;               // nu a fost gasita

  n--;        // in arbore va fi cu un varf mai putin
  k = z->key; // k va retine intreaga informatie din z

  //  - y este z daca z are cel mult un fiu si
  //      succesorul lui z daca z are doi fii
  //  - x este fiul lui y sau 0 daca y nu are fii
  varf<E> *y, *x;

  y = z->st == 0 || z->dr == 0? z: _succ( z );
  x = y->st != 0?           y->st: y->dr;

  // se elimina varful y din arbore astfel:
  //  1. se stabileste legatura in x spre varful tata
  if ( x != 0 )
    x->tata = y->tata;

  //  2. in varful tata se stabileste legatura spre x
  if ( y->tata == 0 )                   root = x;
  else   if ( y == y->tata->st ) y->tata->st = x;
         else                    y->tata->dr = x;

  //  3. daca z are 2 fii, succesorul lui ii ia locul
  if ( y != z ) { z->key = y->key; z->p = y->p; }

  //  4. stergerea propriu-zisa
  y->st = y->dr = 0;
  delete y;

  return 1;
}

Complexitatea functiei de stergere este tipica pentru structurile de cautare. Aceste structuri tind sa devina atat de compacte in organizarea lor interna, incat stergerea fiecarei chei necesita reparatii destul de complicate. De aceea, deseori se prefera o “stergere lenesa” (lazy deletion), prin care varful este doar marcat ca “sters”, stergerea efectiva realizandu-se cu ocazia unor reorganizari periodice.

Desi clasa arbore<E> este incomplet specificata, lipsind constructorul de copiere, operatorul de atribuire, destructorul etc, operatiile implementate in aceasta sectiune pot fi testate prin urmatorul program.

#include <iostream.h>
#include "arbore.h"

main( ) {
  int n;
  cout << "Numarul de varfuri ... "; cin >> n;

  arbore<char> g; char c; float f;

  cout << "Cheile si Frecventele lor:\n";
  for ( int i = 0; i < n; i++ ) {
    cout << "... ";
    cin >> c; cin >> f;
    g.ins( c, f );
  }

  cout << "Arborele initial:\n";     g.inord( );

  cout << "\n\nDelete din initial (cheie) <EOF>:\n ...";
  while( cin >> c ) {
    if ( g.del( c ) ) {
      cout << "\nSe sterge varful cu cheia: " << c;
      cout << "\nInordine:\n"; g.inord( );
    }
    else
      cout << "\nelement absent";
    cout << "\n... ";
  }
  cin.clear( );

  g.re_greedy( );
  cout << "\n\nArborele Greedy:\n";  g.inord( );

  cout << "\n\nInsert in Greedy "
       << "(cheie+frecventa) <EOF>:\n... ";
  while( (cin >> c) && (cin >> f) ) {
    g.ins( c, f );
    cout << "\nInordine:\n"; g.inord( );
    cout << "\n... ";
  }
  cin.clear( );

  cout << "\n\nCautari in Greedy (cheie) <EOF>:\n ...";
  while( cin >> c ) {
    if ( g.search( c ) ) {
      cout << "\nNodul cu cheia: " << c;
      cout << "\nInordine:\n"; g.inord( );
    }
    else
      cout << "\nelement absent";
    cout << "\n... ";
  }
  cin.clear( );

  cout << "\n\nDelete din Greedy (cheie) <EOF>:\n ...";
  while( cin >> c ) {
    if ( g.del( c ) ) {
      cout << "\nSe sterge varful cu cheia: " << c;
      cout << "\nInordine:\n"; g.inord( );
    }
    else
      cout << "\nelement absent";
    cout << "\n... ";
  }
  cin.clear( );

  g.re_prodin( );
  cout << "Arborele Greedy re-ProgDin:\n"; g.inord( );

  return 1;
}

Functia arbore<E>::inord(), definita in Sectiunea 9.2, realizeaza afisarea arborelui, astfel incat sa poata fi usor de reconstituit pe hartie. De exemplu, arborele din Figura 8.8b este afisat astfel:

0x166c ( key C, f 0, st 0x0000, dr 0x0000, tata 0x163c )
0x163c ( key H, f 0, st 0x166c, dr 0x165c, tata 0x0000 )
0x169c ( key M, f 0, st 0x0000, dr 0x0000, tata 0x168c )
0x168c ( key N, f 0, st 0x169c, dr 0x16ac, tata 0x165c )
0x16ac ( key P, f 0, st 0x0000, dr 0x0000, tata 0x168c )
0x165c ( key R, f 0, st 0x168c, dr 0x0000, tata 0x163c )

8.8 Programarea dinamica comparata cu tehnica greedy

Atat programarea dinamica, cat si tehnica greedy, pot fi folosite atunci cand solutia unei probleme este privita ca rezultatul unei secvente de decizii. Deoarece principiul optimalitatii poate fi exploatat de ambele metode, s-ar putea sa fim tentati sa elaboram o solutie prin programare dinamica, acolo unde este suficienta o solutie greedy, sau sa aplicam in mod eronat o metoda greedy, atunci cand este necesara de fapt aplicarea programarii dinamice. Vom considera ca exemplu o problema clasica de optimizare.

Un hot patrunde intr-un magazin si gaseste n obiecte, un obiect i avand valoarea v_i si greutatea g_i. Cum sa-si optimizeze hotul profitul, daca poate transporta cu un rucsac cel mult o greutate G? Deosebim doua cazuri. In primul dintre ele, pentru orice obiect i, se poate lua orice fractiune 0 £ x_i £ 1 din el, iar in al doilea caz, x_i Î {0,1}, adica orice obiect poate fi incarcat numai in intregime in rucsac. Corespunzator acestor doua cazuri, obtinem problema continua a rucsacului, respectiv, problema 0/1 a rucsacului. Evident, hotul va selecta obiectele astfel incat sa maximizeze functia obiectiv

unde x = (x₁, x₂, ..., x_n), verifica conditia

Solutia problemei rucsacului poate fi privita ca rezultatul unei secvente de decizii. De exemplu, hotul va decide pentru inceput asupra valorii lui x₁, apoi asupra valorii lui x₂ etc. Printr-o secventa optima de decizii, el va incerca sa maximizeze functia obiectiv. Se observa ca este valabil principiul optimalitatii. Ordinea deciziilor poate fi desigur oricare alta.

Problema continua a rucsacului se poate rezolva prin metoda greedy, selectand la fiecare pas, pe cat posibil in intregime, obiectul pentru care v_i/g_i este maxim. Fara a restrange generalitatea, vom presupune ca

v₁/g₁ ³ v₂/g₂ ³ ... ³ v_n/g_n

Puteti demonstra ca prin acest algoritm obtinem solutia optima si ca aceasta este de forma x^* = (1, ..., 1,  , 0, ..., 0), k fiind un indice, 1 £ k £ n, astfel incat 0 £ x_k £ 1. Algoritmul greedy gaseste secventa optima de decizii, luand la fiecare pas cate o decizie care este optima local. Algoritmul este corect, deoarece nici o decizie din secventa nu este eronata. Daca nu consideram timpul necesar sortarii initiale a obiectelor, timpul este in ordinul lui n.

Sa trecem la problema 0/1 a rucsacului. Se observa imediat ca tehnica greedy nu conduce in general la rezultatul dorit. De exemplu, pentru g = (1, 2, 3), v = (6, 10, 12), G = 5, algoritmul greedy furnizeaza solutia (1, 1, 0), in timp ce solutia optima este (0, 1, 1). Tehnica greedy nu poate fi aplicata, deoarece este generata o decizie (x₁ = 1) optima local, nu insa si global. Cu alte cuvinte, la primul pas, nu avem suficienta informatie locala pentru a decide asupra valorii lui x₁. Strategia greedy exploateaza insuficient principiul optimalitatii, considerand ca intr-o secventa optima de decizii fiecare decizie (si nu fiecare subsecventa de decizii, cum procedeaza programarea dinamica) trebuie sa fie optima. Problema se poate rezolva printr-un algoritm de programare dinamica, in aceasta situatie exploatandu-se complet principiul optimalitatii. Spre deosebire de problema continua, nu se cunoaste nici un algoritm polinomial pentru problema 0/1 a rucsacului.

Diferenta esentiala dintre tehnica greedy si programarea dinamica consta in faptul ca metoda greedy genereaza o singura secventa de decizii, exploatand incomplet principiul optimalitatii. In programarea dinamica, se genereaza mai multe subsecvente de decizii; tinand cont de principiul optimalitatii, se considera insa doar subsecventele optime, combinandu-se acestea in solutia optima finala. Cu toate ca numarul total de secvente de decizii este exponential (daca pentru fiecare din cele n decizii sunt d posibilitati, atunci sunt posibile d ⁿ secvente de decizii), algoritmii de programare dinamica sunt de multe ori polinomiali, aceasta reducere a complexitatii datorandu-se utilizarii principiului optimalitatii. O alta caracteristica importanta a programarii dinamice este ca se memoreaza subsecventele optime, evitandu-se astfel recalcularea lor.

8.9 Exercitii

8.1       Demonstrati ca numarul total de apeluri recursive necesare pentru a-l calcula pe C(n, k) este 2  - 2.

Solutie: Notam cu r(n, k) numarul de apeluri recursive necesare pentru a-l calcula pe C(n, k). Procedam prin inductie, in functie de n. Daca n este 0, proprietatea este adevarata. Presupunem proprietatea adevarata pentru n-1 si demonstram pentru n.

Presupunem, pentru inceput, ca 0 < k < n. Atunci, avem recurenta

r(n, k) = r(n-1, k-1) + r(n-1, k) + 2

Din relatia precedenta, obtinem

r(n, k) = 2

- 2 + 2

- 2 + 2 = 2

- 2

Daca k este 0 sau n, atunci r(n, k) = 0 si, deoarece in acest caz avem  = 1, rezulta ca proprietatea este adevarata. Acest rezultat poate fi verificat practic, ruland programul din Exercitiul 2.5.

8.2       Aratati ca principiul optimalitatii

i)     este valabil in problema gasirii celui mai scurt drum dintre doua varfuri ale unui graf
ii)    nu este valabil in problema determinarii celui mai lung drum simplu dintre doua varfuri ale unui graf

8.3       Demonstrati ca  ³ 4ⁿ/(2n+1).

8.4       Folosind algoritmul serie, calculati probabilitatea ca jucatorul A sa castige, presupunand n = 4 si p = 0,45.

8.5       Problema inmultirii inlantuite optime a matricilor se poate rezolva si prin urmatorul algoritm recursiv:

function rminscal(i, j)
     {returneaza numarul minim de inmultiri scalare
       pentru a calcula produsul matricial M_i  M_i+1 ... M_j}
     if i = j then return 0
     q ¬ +¥
     for k ¬ i to j-1 do
          q ¬ min(q, rminscal(i, k)+rminscal(k+1, j)+d[i-1]d[k]d[ j])
     return q

unde tabloul d[0 .. n] este global. Gasiti o limita inferioara a timpului. Explicati ineficienta acestui algoritm.

Solutie: Notam cu r( j-i+1) numarul de apeluri recursive necesare pentru a-l calcula pe rminscal(i, j). Pentru n > 2 avem

iar r(2) = 2. Prin metoda iteratiei, deduceti ca r(n) ³ 2^n-1, pentru n > 2. Timpul pentru un apel rminscal(1, n) este atunci in W(2ⁿ).

8.6       Elaborati un algoritm eficient care sa afiseze parantezarea optima a unui produs matricial M(1), ..., M(n). Folositi pentru aceasta matricea r, calculata de algoritmul minscal. Analizati algoritmul obtinut.

Solutie: Se apeleaza cu paran(1, n) urmatorul algoritm:

function paran(i, j)
     if  i = j   then   write “M(”, i, “)”
                   else   write “(”
                   parant(i, r[i, j])
                   write “*”
                   parant(r[i, j]+1, j)
                   write “)”

Aratati prin inductie ca o parantezare completa unei expresii de n elemente are exact n-1 perechi de paranteze. Deduceti de aici care este eficienta algoritmului.

8.7       Presupunand matricea P din algoritmul lui Floyd cunoscuta, elaborati un algoritm care sa afiseze prin ce varfuri trece cel mai scurt drum dintre doua varfuri oarecare.

8.8       Intr-un graf orientat, sa presupunem ca ne intereseaza doar existenta, nu si lungimea drumurilor, intre fiecare pereche de varfuri. Initial, L[i, j] = true daca muchia (i, j) exista si L[i, j] = false in caz contrar. Modificati algoritmul lui Floyd astfel incat, in final, sa avem D[i, j] = true daca exista cel putin un drum de la i la j si D[i, j] = false in caz contrar.

Solutie: Se inlocuieste bucla cea mai interioara cu:

D[i, j] ¬ D[i, j] or (D[i, k] and D[k, j])

obtinandu-se algoritmul lui Warshall (1962). Matricea booleana L se numeste inchiderea tranzitiva a grafului.

8.9       Aratati cu ajutorul unui contraexemplu ca urmatoarea propozitie nu este, in general, adevarata: “Un arbore binar este un arbore de cautare daca cheia fiecarui varf neterminal este mai mare sau egala cu cheia fiului sau stang si mai mica sau egala cu cheia fiului sau drept”.

8.10     Fie un arbore binar de cautare reprezentat prin adrese, astfel incat varful i (adica varful a carui adresa este i) este memorat in patru locatii diferite continand :

                            KEY[i]    =   cheia varfului
                            ST[i]       =   adresa fiului stang
                            DR[i]      =   adresa fiului drept
                            TATA[i]  =   adresa tatalui

(Daca se foloseste o implementare prin tablouri paralele, atunci adresele sunt indici de tablou). Presupunem ca variabila root contine adresa radacinii arborelui si ca o adresa este zero, daca si numai daca varful catre care se face trimiterea lipseste. Elaborati algoritmi pentru urmatoarele operatii in arborele de cautare:

i)     Determinarea varfului care contine o cheie v data. Daca un astfel de varf nu exista, se va returna adresa zero.
ii)    Determinarea varfului care contine cheia minima.
iii)  Determinarea succesorului unui varf i dat (succesorul varfului i este varful care are cea mai mica cheie mai mare decat KEY[i]).

Care este eficienta acestor algoritmi?

Solutie:

i)     Apelam tree-search(root, v), tree-search fiind functia:

function tree-search(i, v)
     if i = 0 or v = KEY[i] then return i
     if v < KEY[i]    then   return tree-search(ST[i], v)
                            else   return tree-search(DR[i], v)

Iata si o versiune iterativa a acestui algoritm:

function iter-tree-search(i, v)
     while i ¹ 0 and v ¹ KEY[i] do
          if i < KEY[i]    then   i ¬ ST[i]
                                 else   i ¬ DR[i]
     return i

ii)    Se apeleaza tree-min(root), tree-min fiind functia:

function tree-min(i)
     while ST[i] ¹ 0 do i ¬ ST[i]
     return i

iii)  Urmatorul algoritm returneaza succesorul varfului i:

function tree-succesor(i)
     if DR[i] ¹ 0 then return tree-min(DR[i])
     j ¬ TATA[i]
     while j ¹ 0 and i = DR[ j]  do   i ¬ j
                                                    j ¬ TATA[ j]
     return j

8.11     Gasiti o formula explicita pentru T(n), unde T(n) este numarul de arbori de cautare diferiti care se pot construi cu n chei distincte.

Indicatie: Faceti legatura cu problema inmultirii inlantuite a matricilor.

8.12     Exista un algoritm greedy evident pentru a construi arborele optim de cautare avand cheile c₁ < c₂ < ... < c_n: se plaseaza cheia cea mai probabila, c_k, la radacina si se construiesc subarborii sai stang si drept pentru cheile c₁, c₂, ..., c_k-1, respectiv, c_k+1, c_k+2, ..., c_n, in mod recursiv, pe acelasi principiu.

i)     Cat timp necesita algoritmul pentru cazul cel mai nefavorabil?
ii)    Aratati pe baza unui contraexemplu ca prin acest algoritm greedy nu se obtine intotdeauna arborele optim de cautare.

8.13     Un subcaz oarecare al problemei 0/1 a rucsacului se poate formula astfel:

Sa se gaseasca

unde maximul se ia pentru toti vectorii (x_l, ..., x_j) pentru care

x_i Î {0, 1},    l £ i £ j

In particular, V(1, n, G) este valoarea maxima care se poate incarca in rucsac in cazul problemei initiale. O solutie a acestei probleme se poate obtine daca consideram ca deciziile se iau retrospectiv, adica in ordinea x_n, x_n-1, ..., x₁. Principiul optimalitatii este valabil si avem

V(1, n, G) = max(V(1, n-1, G), V(1, n-1, G-g_n) + v_n )

si, in general,

V(1, j, X) = max(V(1, j-1, X), V(1, j-1, X-g_j ) + v_j)

unde V(1, 0, X) = 0 pentru X ³ 0, iar V(1, j, X) = -¥ pentru X < 0. De aici se poate calcula, prin tehnica programarii dinamice, valoarea V(1, n, G) care ne intereseaza.

Gasiti o recurenta similara pentru situatia cand deciziile se iau prospectiv, adica in ordinea x₁, x₂, ..., x_n.

8.14     Am vazut (in Sectiunea 6.1) ca tehnica greedy poate fi aplicata in problema determinarii restului cu un numar minim de monezi doar pentru anumite cazuri particulare. Problema se poate rezolva, in cazul general, prin metoda programarii dinamice.

Sa presupunem ca avem un numar finit de n tipuri de monezi, fiecare in numar nelimitat, iar tabloul M[1 .. n] contine valoarea acestor monezi. Fie S suma pe care dorim sa o obtinem, folosind un numar minim de monezi.

i)     In tabloul C[1 .. n, 1 .. S], fie C[i, j] numarul minim de monezi necesare pentru a obtine suma j, folosind doar monezi de tipul M[1], M[2], ..., M[i], unde C[i, j] = +¥, daca suma j nu poate fi obtinuta astfel. Gasiti o recurenta pentru C[i, j].
ii)    Elaborati un algoritm care foloseste tehnica programarii dinamice pentru a calcula valorile C[n, j], 1 £ j £ S. Algoritmul trebuie sa utilizeze un singur vector de S elemente. Care este timpul necesar, in functie de n si S?
iii)  Gasiti un algoritm greedy care determina cum se obtine suma S cu un numar minim de monezi, presupunand cunoscute valorile C[n, j].

8.15     Fie u si v doua secvente de caractere. Dorim sa transformam pe u in v, cu un numar minim de operatii de urmatoarele tipuri:

·    sterge un caracter
·    adauga un caracter
·    schimba un caracter

De exemplu, putem sa transformam abbac in abcbc in trei etape:

          abbac  ®    abac         (sterge b)
                     ®    ababc       (adauga b)
                     ®    abcbc       (schimba a cu c)

Aratati ca aceasta transformare nu este optima. Elaborati un algoritm de programare dinamica care gaseste numarul minim de operatii necesare (si le specifica) pentru a-l transforma pe u in v.

8.16     Sa consideram alfabetul S = {a, b, c}. Pentru elementele lui S definim urmatoarea tabla de inmultire:

Observati ca inmultirea definita astfel nu este nici comutativa si nici asociativa. Gasiti un algoritm eficient care examineaza sirul x = x₁ x₂ ... x_n de caractere ale lui S si decide daca x poate fi parantezat astfel incat expresia rezultata sa fie a. De exemplu, daca x = bbbba, algoritmul trebuie sa returneze “da” deoarece (b(bb))(ba) = a.

8.17     Aratati ca numarul de moduri in care un poligon convex cu n laturi poate fi partitionat in n-2 triunghiuri, folosind linii diagonale care nu se intretaie, este T(n-1), unde T(n-1) este al (n-1)-lea numar catalan.

[*]    Problema inmultirii inlantuite optime a matricilor poate fi rezolvata si prin algoritmi mai eficienti. Astfel, T. C. Hu si M. R. Shing au propus, (in 1982 si 1984),  un algoritm cu timpul de executie in O(n log n).

[**]   Diagonala principala este diagonala care uneste coltul din stanga sus cu cel din dreapta jos.

[***]   In aceasta sectiune vom subintelege ca toti arborii de cautare sunt binari.

[****]   Daca tinem cont de imbunatatirile propuse de D. E. Knuth (“Tratat de programarea calculatoarelor. Sortare si cautare”, Sectiunea 6.2.2), acest algoritm de construire a arborilor optimi de cautare poate fi facut patratic.

[*****]             In procesul de optimizare pot fi implicate nu numai cautarile terminate cu succes, ci si cele nereusite. Cautarea cheilor care nu sunt in arbore este tot atat de costisitoare ca si cautarea celor care sunt in arbore. Pentru detalii asupra acestei probleme se poate consulta D. E. Knuth, “Tratat de programarea calculatoarelor. Sortare si cautare”,  Sectiunea 6.2.2.

[******]             Acest procedeu de estimare a probabilitatilor printr-un proces de instruire poate fi formalizat intr-un cadru matematic riguros (R. Andonie, “A Converse H-Theorem for Inductive Processes”, Computers and Artificial Intelligence, Vol. 9, 1990, No. 2, pp. 159-167).

[*******]             Succesorul unui varf X este varful cu cea mai mica cheie mai mare decat cheia varfului X (vezi si Exercitiul 8.10).

[********]             Predecesorul unui varf X este varful care are cea mai mare cheie mai mica decat cheia varfului X.