7. Algoritmi divide et impera
  7.1 Tehnica divide et impera
  7.2 Cautarea binara
  7.3 Mergesort (sortarea prin interclasare)
  7.4 Mergesort in clasele tablou<T> si lista<E>
    7.4.1 O solutie neinspirata
    7.4.2 Tablouri sortabile si liste sortabile
  7.5 Quicksort (sortarea rapida)
  7.6 Selectia unui element dintr-un tablou
  7.7 O problema de criptologie
  7.8 Inmultirea matricilor
  7.9 Inmultirea numerelor intregi mari
  7.10 Exercitii

7. Algoritmi divide et impera

7.1 Tehnica divide et impera

Divide et impera este o tehnica de elaborare a algoritmilor care consta in:

·    Descompunerea cazului ce trebuie rezolvat intr-un numar de subcazuri mai mici ale aceleiasi probleme.
·    Rezolvarea succesiva si independenta a fiecaruia din aceste subcazuri.
·    Recompunerea subsolutiilor astfel obtinute pentru a gasi solutia cazului initial.

Sa presupunem ca avem un algoritm A cu timp patratic. Fie c o constanta, astfel incat timpul pentru a rezolva un caz de marime n este t_A(n) £ cn². Sa presupunem ca este posibil sa rezolvam un astfel de caz prin descompunerea in trei subcazuri, fiecare de marime én/2ù. Fie d o constanta, astfel incat timpul necesar pentru descompunere si recompunere este t(n) £ dn. Folosind vechiul algoritm si ideea de descompunere-recompunere a subcazurilor, obtinem un nou algoritm B, pentru care:

t_B(n) = 3t_A(én/2ù)+t(n) £ 3c((n+1)/2)²+dn = 3/4cn²+(3/2+d)n+3/4c

Termenul 3/4cn² domina pe ceilalti cand n este suficient de mare, ceea ce inseamna ca algoritmul B este in esenta cu 25% mai rapid decat algoritmul A. Nu am reusit insa sa schimbam ordinul timpului, care ramane patratic.

Putem sa continuam in mod recursiv acest procedeu, impartind subcazurile in subsubcazuri etc. Pentru subcazurile care nu sunt mai mari decat un anumit prag n₀, vom folosi tot algoritmul A. Obtinem astfel algoritmul C, cu timpul

Conform rezultatelor din Sectiunea 5.3.5, t_C(n) este in ordinul lui n^lg 3. Deoarece lg 3 @ 1,59, inseamna ca de aceasta data am reusit sa imbunatatim ordinul timpului.

Iata o descriere generala a metodei divide et impera:

function divimp(x)
     {returneaza o solutie pentru cazul x}
     if x este suficient de mic then return adhoc(x)
     {descompune x in subcazurile x₁, x₂, …, x_k}
     for i ¬ 1 to k do y_i ¬ divimp(x_i)
     {recompune y₁, y₂, …, y_k in scopul obtinerii solutiei y pentru x}
     return y

unde adhoc este subalgoritmul de baza folosit pentru rezolvarea micilor subcazuri ale problemei in cauza (in exemplul nostru, acest subalgoritm este A).

Un algoritm divide et impera trebuie sa evite descompunerea recursiva a subcazurilor “suficient de mici”, deoarece, pentru acestea, este mai eficienta aplicarea directa a subalgoritmului de baza. Ce inseamna insa “suficient de mic”?

In exemplul precedent, cu toate ca valoarea lui n₀ nu influenteaza ordinul timpului, este influentata insa constanta multiplicativa a lui n^lg 3, ceea ce poate avea un rol considerabil in eficienta algoritmului. Pentru un algoritm divide et impera oarecare, chiar daca ordinul timpului nu poate fi imbunatatit, se doreste optimizarea acestui prag in sensul obtinerii unui algoritm cat mai eficient. Nu exista o metoda teoretica generala pentru aceasta, pragul optim depinzand nu numai de algoritmul in cauza, dar si de particularitatea implementarii. Considerand o implementare data, pragul optim poate fi determinat empiric, prin masurarea timpului de executie pentru diferite valori ale lui n₀ si cazuri de marimi diferite.

In general, se recomanda o metoda hibrida care consta in: i) determinarea teoretica a formei ecuatiilor recurente; ii) gasirea empirica a valorilor constantelor folosite de aceste ecuatii, in functie de implementare.

Revenind la exemplul nostru, pragul optim poate fi gasit rezolvand ecuatia

t_A(n) = 3t_A(én/2ù) + t(n)

Empiric, gasim n₀ @ 67, adica valoarea pentru care nu mai are importanta daca aplicam algoritmul A in mod direct, sau daca continuam descompunerea. Cu alte cuvinte, atata timp cat subcazurile sunt mai mari decat n₀, este bine sa continuam descompunerea. Daca continuam insa descompunerea pentru subcazurile mai mici decat n₀, eficienta algoritmului scade.

Observam ca metoda divide et impera este prin definitie recursiva. Uneori este posibil sa eliminam recursivitatea printr-un ciclu iterativ. Implementata pe o masina conventionala, versiunea iterativa poate fi ceva mai rapida (in limitele unei constante multiplicative). Un alt avantaj al versiunii iterative ar fi faptul ca economiseste spatiul de memorie. Versiunea recursiva foloseste o stiva necesara memorarii apelurilor recursive. Pentru un caz de marime n, numarul apelurilor recursive este de multe ori in W(log n), uneori chiar in W(n).

7.2 Cautarea binara

Cautarea binara este cea mai simpla aplicatie a metodei divide et impera, fiind cunoscuta inca inainte de aparitia calculatoarelor. In esenta, este algoritmul dupa care se cauta un cuvint intr-un dictionar, sau un nume in cartea de telefon.

Fie T[1 .. n] un tablou ordonat crescator si x un element oarecare. Problema consta in a-l gasi pe x in T, iar daca nu se afla acolo in a gasi pozitia unde poate fi inserat. Cautam deci indicele i astfel incat 1 £ i £ n si T[i] £ x < T[i+1], cu conventia T[0] = -¥, T[n+1] = +¥. Cea mai evidenta metoda este cautarea secventiala:

function sequential(T[1 .. n], x)
     {cauta secvential pe x in tabloul T }
     for i ¬ 1 to n do
          if T[i] > x then return i-1
     return n

Algoritmul necesita un timp in Q(1+r), unde r este indicele returnat; aceasta inseamna Q(1) pentru cazul cel mai favorabil si Q(n) pentru cazul cel mai nefavorabil. Daca presupunem ca elementele lui T sunt distincte, ca x este un element al lui T si ca se afla cu probabilitate egala in oricare pozitie din T, atunci bucla for se executa in medie de (n²+3n-2)/2n ori. Timpul este deci in Q(n) si pentru cazul mediu.

Pentru a mari viteza de cautare, metoda divide et impera sugereaza sa-l cautam pe x fie in prima jumatate a lui T, fie in cea de-a doua. Comparandu-l pe x cu elementul din mijlocul tabloului, putem decide in care dintre jumatati sa cautam. Repetand recursiv procedeul, obtinem urmatorul algoritm de cautare binara:

function binsearch(T[1 .. n], x)
     {cauta binar pe x in tabloul T}
     if n = 0 or x < T[1] then return 0
     return binrec(T[1 .. n], x)

function binrec(T[i .. j], x)
     {cauta binar pe x in subtabloul T[i .. j]; aceasta procedura
       este apelata doar cand T[i] £ x < T[ j+1] si i £ j}
     if i = j then return i
     k ¬ (i+j+1) div 2
     if x < T[k]   then   return binrec(T[i .. k-1], x)
                        else   return binrec(T[k .. j], x)

Algoritmul binsearch necesita un timp in Q(log n), indiferent de pozitia lui x in T (demonstrati acest lucru, revazand Sectiunea 5.3.5). Procedura binrec executa doar un singur apel recursiv, in functie de rezultatul testului “x < T[k]”. Din aceasta cauza, cautarea binara este, mai curand, un exemplu de simplificare, decat de aplicare a tehnicii divide et impera.

Iata si versiunea iterativa a acestui algoritm:

function iterbin1(T[1 .. n], x)
     {cautare binara iterativa}
     if n = 0 or x < T[1] then return 0
     i ¬ 1; j ¬ n
     while i < j do
          {T[i] £ x < T[ j+1]}
          k ¬ (i+j+1) div 2
          if x < T[k]   then   j ¬ k-1
                            else   i ¬ k
     return i

Acest algoritm de cautare binara pare ineficient in urmatoarea situatie: daca la un anumit pas avem x = T[k], se continua totusi cautarea. Urmatorul algoritm evita acest inconvenient, oprindu-se imediat ce gaseste elementul cautat.

function iterbin2(T[1 .. n], x)
     {varianta a cautarii binare iterative}
     if n = 0 or x < T[1] then return 0
     i ¬ 1; j ¬ n
     while i < j do
          {T[i] £ x < T[ j+1]}
          k ¬ (i+j) div 2
          case  x < T[k]: j ¬ k-1
                   x ³ T[k+1]:  i ¬ k+1
                   otherwise:   i, j ¬ k
     return i

Timpul pentru iterbin1 este in Q(log n). Algoritmul iterbin2 necesita un timp care depinde de pozitia lui x in T, fiind in Q(1), Q(log n), Q(log n) pentru cazurile cel mai favorabil, mediu si respectiv, cel mai nefavorabil.

Care din acesti doi algoritmi este oare mai eficient? Pentru cazul cel mai favorabil, iterbin2 este, evident, mai bun. Pentru cazul cel mai nefavorabil, ordinul timpului este acelasi, numarul de executari ale buclei while este acelasi, dar durata unei bucle while pentru iterbin2 este ceva mai mare; deci iterbin1 este preferabil, avand constanta multiplicativa mai mica. Pentru cazul mediu, compararea celor doi algoritmi este mai dificila: ordinul timpului este acelasi, o bucla while in iterbin1 dureaza in medie mai putin decat in iterbin2, in schimb iterbin1 executa in medie mai multe bucle while decat iterbin2.

7.3 Mergesort (sortarea prin interclasare)

Fie T[1 .. n] un tablou pe care dorim sa-l sortam crescator. Prin tehnica divide et impera putem proceda astfel: separam tabloul T in doua parti de marimi cat mai apropiate, sortam aceste parti prin apeluri recursive, apoi interclasam solutiile pentru fiecare parte, fiind atenti sa pastram ordonarea crescatoare a elementelor. Obtinem urmatorul algoritm:

procedure mergesort(T[1 .. n])
     {sorteaza in ordine crescatoare tabloul T}
     if n este mic
          then  insert(T)
          else   arrays U[1 .. n div 2], V[1 .. (n+1) div 2]
                   U ¬ T[1 .. n div 2]
                   V ¬ T[1 + (n div 2) .. n]
                   mergesort(U); mergesort(V)
     merge(T, U, V)

unde insert(T) este algoritmul de sortare prin insertie cunoscut, iar merge(T, U, V) interclaseaza intr-un singur tablou sortat T cele doua tablouri deja sortate U si V.

Algoritmul mergesort ilustreaza perfect principiul divide et impera: pentru n avand o valoare mica, nu este rentabil sa apelam recursiv procedura mergesort, ci este mai bine sa efectuam sortarea prin insertie. Algoritmul insert lucreaza foarte bine pentru n £ 16, cu toate ca, pentru o valoare mai mare a lui n, devine neconvenabil. Evident, se poate concepe un algoritm mai putin eficient, care sa mearga pana la descompunerea totala; in acest caz, marimea stivei este in Q(log n).

Spatiul de memorie necesar pentru tablourile auxiliare U si V este in Q(n). Mai precis, pentru a sorta un tablou de n = 2^k elemente, presupunand ca descompunerea este totala, acest spatiu este de

elemente.

Putem considera (conform Exercitiului 7.7) ca algoritmul merge(T, U, V) are timpul de executie in Q(#U + #V), indiferent de ordonarea elementelor din U si V. Separarea lui T in U si V necesita tot un timp in Q(#U + #V). Timpul necesar algoritmului mergesort pentru a sorta orice tablou de n elemente este atunci t(n) Î t(ën/2û)+t(én/2ù)+Q(n). Aceasta ecuatie, pe care am analizat-o in Sectiunea 5.1.2, ne permite sa conchidem ca timpul pentru mergesort este in Q(n log n). Sa reamintim timpii celorlalti algoritmi de sortare, algoritmi analizati in Capitolul 5: pentru cazul mediu si pentru cazul cel mai nefavorabil insert si select necesita un timp in Q(n²), iar heapsort un timp in Q(n log n).

In algoritmul mergesort, suma marimilor subcazurilor este egala cu marimea cazului initial. Aceasta proprietate nu este in mod necesar valabila pentru algoritmii divide et impera. Oare de ce este insa important ca subcazurile sa fie de marimi cat mai egale? Daca in mergesort il separam pe T in tabloul U avand n-1 elemente si tabloul V avand un singur element, se obtine (Exercitiul 7.9) un nou timp de executie, care este in Q(n²). Deducem de aici ca este esential ca subcazurile sa fie de marimi cat mai apropiate (sau, alfel spus, subcazurile sa fie cat mai echilibrate).

7.4 Mergesort in clasele tablou<T> si lista<E>

7.4.1 O solutie neinspirata

Desi eficient in privinta timpului, algoritmul de sortare prin interclasare are un handicap important in ceea ce priveste memoria necesara. Intr-adevar, orice tablou de n elemente este sortat intr-un timp in Q(n log n), dar utilizand un spatiu suplimentar de memorie[*] de 2n elemente. Pentru a reduce consumul de memorie, in implementarea acestui algoritm nu vom utiliza variabilele intermediare U si V de tip tablou<T>, ci o unica zona de auxiliara de n elemente.

Convenim sa implementam procedura mergesort din Sectiunea 7.3 ca membru private al clasei parametrice tablou<T>. Invocarea acestei proceduri se va realiza prin functia membra

template <class T>
tablou<T>& tablou<T>::sort( ) {
  T *aux = new T[ d ];    // alocarea zonei de interclasare
  mergesort( 0, d, aux ); //       si sortarea propriu-zisa
  delete [ ] aux;         // eliberarea zonei alocate

  return *this;
}

Am preferat aceasta maniera de “incapsulare” din urmatoarele doua motive:

·    Alocarea si eliberarea spatiului suplimentar necesar interclasarii se face o singura data, inainte si dupa terminarea sortarii. Functia mergesort(), ca functie recursiva, nu poate avea controlul asupra alocarii si eliberarii acestei zone.
·    Algoritmul mergesort are trei parametri care pot fi ignorati la apelarea functiei de sortare. Acestia sunt: adresa zonei suplimentare de memorie si cei doi indici prin care se incadreaza elementele de sortat din tablou.

Dupa cum se poate vedea in Exercitiul 7.7, implementarea interclasarii se simplifica mult prin utilizarea unor valori “santinela” in tablourile de interclasat. Functia mergesort():

template <class T>
void tablou<T>::mergesort( int st, int dr, T *x ) {
  if ( dr - st > 1 ) {
    // mijlocul intervalului
    int m = ( st + dr ) / 2;

    // sortarea celor doua parti
    mergesort( st, m );
    mergesort( m, dr );

    // pregatirea zonei x pentru interclasare
    int k = st;
    for ( int i = st; i < m; ) x[ i++ ] = a[ k++ ];
    for ( int j = dr; j > m; ) x[ --j ] = a[ k++ ];

    // interclasarea celor doua parti din x in zona a
    i = st; j = dr - 1;
    for ( k = st; k < dr; k++ )
    a[ k ] = x[ j ] > x[ i ]? x[ i++ ]: x[ j-- ];
  }
}

se adapteaza surprinzator de simplu la utilizarea “santinelelor”. Nu avem decat sa transferam in zona auxiliara cele doua jumatati deja sortate, astfel incat valorile maxime sa fie la mijlocul acestei zone. Altfel spus, prima jumatate va fi transferata crescator, iar cea de-a doua descrescator, in continuarea primei jumatati. Incepand interclasarea cu valorile minime, valoarea maxima din fiecare jumatate este santinela pentru cealalta jumatate.

Sortarea prin interclasare prezinta un avantaj foarte important fata de alte metode de sortare deoarece elementele de sortat sunt parcurse secvential, element dupa element. Din acest motiv, metoda este potrivita pentru sortarea fisierelor sau listelor. De exemplu, procedura de sortare prin interclasare a obiectelor de tip lista<E>

template <class E>
lista<E>& lista<E>::sort() {
  if ( head )
    head = mergesort( head );

  return *this;
}

rearanjeaza nodurile in ordinea crescatoare a cheilor, fara a folosi noduri sau liste temporare. Pretul in spatiu suplimentar de memorie este totusi platit, deoarece orice lista inlantuita necesita memorie in ordinul numarului de elemente pentru realizarea inlantuirii.

Conform algoritmului mergesort, lista se imparte in doua parti egale, iar dupa sortarea fiecareia se realizeaza interclasarea. Impartirea listei in cele doua parti egale nu se poate realiza direct, ca in cazul tablourilor, ci in mai multi pasi. Astfel, vom parcurge lista pana la sfarsit, pentru a putea determina elementul din mijloc. Apoi stabilim care este elementul din mijloc si, in final, izolam cele doua parti, fiecare in cate o lista. In functia mergesort():

template <class E>
nod<E>* mergesort ( nod<E> *c ) {
  if ( c && c->next ) {
    // sunt cel putin doua noduri in lista
    nod<E> *a = c, *b;

    for ( b = c->next; b; a = a->next )
      if ( b->next ) b = b->next->next;
      else           break;
    b = a->next; a->next = 0;
    return merge( mergesort( c ), mergesort( b ) );
  }
  else
    // lista contine cel mult un nod
    return c;
}

impartirea listei se realizeaza printr-o singura parcurgere, dar cu doua adrese de noduri, a si b. Principiul folosit este urmatorul: daca b inainteaza in parcurgerea listei de doua ori mai repede decat a, atunci cand b a ajuns la ultimul nod, a este la nodul de mijloc al listei.

Spre deosebire de algoritmul mergesort, sortarea listelor prin interclasare nu deplaseaza valorile de sortat. Functia merge() interclaseaza listele de la adresele a si b prin simpla modificare a legaturilor nodurilor.

template <class E>
nod<E>* merge( nod<E> *a, nod<E> *b ) {
  nod<E> *head;           // primul nod al listei interclasate

  if ( a && b )
    // ambele liste sunt nevide;
    // stabilim primul nod din lista interclasata
    if ( a->val > b->val ) { head = b; b = b->next; }
    else                   { head = a; a = a->next; }
  else
    // cel putin una din liste este vida;
    // nu avem ce interclasa
    return a? a: b;

  // interclasarea propriu-zisa
  nod<E> *c = head;       // ultimul nod din lista interclasata
  while ( a && b )
    if ( a->val > b->val ) { c->next = b; c = b; b = b->next; }
    else                   { c->next = a; c = a; a = a->next; }

  // cel putin una din liste s-a epuizat
  c->next = a? a: b;

  // se returneaza primul nod al listei interclasate
  return head;
}

Functia de sortare mergesort(), impreuna cu cea de interclasare merge(), lucreaza exclusiv asupra nodurilor. Deoarece aceste functii sunt invocate doar la nivel de lista, ele nu sunt membre in clasa nod<E>, ci doar friend fata de aceasta clasa. Incapsularea lor este realizata prin mecanismul standard al limbajului C++. Desi aceste functii apartin domeniului global, ele nu pot fi invocate de aici datorita obiectelor de tip nod<E>, obiecte accesibile doar din domeniul clasei lista<E>. Aceasta maniera de incapsulare nu este complet sigura, deoarece, chiar daca nu putem manipula obiecte de tip nod<E>, totusi putem lucra cu adrese de nod<E>. De exemplu, functia

void f( ) {
  mergesort( (nod<int> *)0 );
}

“trece” de compilare, dar efectele ei la rularea programului sunt imprevizibile.

Prezenta functiilor de sortare in tablou<T> si lista<E> (de fapt si in nod<E>) impune completarea claselor T si E cu operatorul de comparare >. Orice tentativa de a defini (atentie, de a defini si nu de a sorta) obiecte de tip tablou<T> sau lista<E> este semnalata ca eroare de compilare, daca tipurile T sau E nu au definit acest operator. Situatia apare, deoarece generarea unei clase parametrice implica generarea tuturor functiilor membre. Deci, chiar daca nu invocam functia de sortare pentru tipul tablou<T>, ea este totusi generata, iar generarea ei necesita operatorul de comparare al tipului T.

De exemplu, pentru a putea lucra cu liste de muchii, lista<muchie>, sau tablouri de tablouri, tablou< tablou<T> >, vom implementa operatorii de comparare pentru clasa muchie si clasa tablou<T>. Muchiile sunt comparate in functie de costul lor, dar cum vom proceda cu tablourile? O solutie este de a lucra conform ordinii lexicografice, adica de a aplica aceeasi metoda care se aplica la ordonarea numelor in cartea de telefoane, sau in catalogul scolar:

template <class T>
operator > ( const tablou<T>& a, const tablou<T>& b ) {
  // minumul elementelor
  int as = a.size( ), bs = b.size( );
  int n = as < bs? as: bs;

  // comparam pana la prima diferenta
  for ( int i = 0; i < n; i++ )
    if ( a[ i ] != b[ i ] ) return a[ i ] > b[ i ];

  // primele n elemente sunt identice
  return as > bs;
}

Atunci cand operatorii de comparare nu prezinta interes, sau nu pot fi definiti, ii putem implementa ca functii inefective. Astfel, daca avem nevoie de un tablou de liste sau de o lista de liste asupra carora nu vom aplica operatii de sortare, va trebui sa definim operatorii inefectivi:

template <class E>
operator >( const lista<E>&, const lista<E>& ) {
  return 1;
}

In concluzie, extinderea claselor tablou<T> si lista<E> cu functiile de sortare nu mentine compatibilitatea acestor clase fata de aplicatiile dezvoltate pana acum. Oricand este posibil ca recompilarea unei aplicatii in care se utilizeaza, de exemplu, tablouri sau liste cu elemente de tip XA, XB etc, sa devina un cosmar, deoarece, chiar daca nu are nici un sens, trebuie sa completam fiecare clasa XA, XB etc, cu operatorul de comparare >.

Programarea orientata pe obiect se foloseste tocmai pentru a evita astfel de situatii, nu pentru a le genera.

7.4.2 Tablouri sortabile si liste sortabile

Sortarea este o operatie care completeaza facilitatile clasei tablou<T>, fara a exclude utilizarea acestei clase pentru tablouri nesortabile. Din acest motiv, functiile de sortare nu pot fi functii membre in clasa tablou<T>.

O solutie posibila de incapsulare a sortarii este de a construi, prin derivare publica din tablou<T>, subtipul tablouSortabil<T>, care sa contina tot ceea ce este necesar pentru sortare. Mecanismului standard de conversie, de la tipul derivat public la tipul de baza, permite ca un tablouSortabil<T> sa poata fi folosit oricand in locul unui tablou<T>.

In continuare, vom prezenta o alta varianta de incapsulare, mai putin clasica, prin care atributul “sortabil” este considerat doar in momentul invocarii functiei de sortatre, nu apriori, prin definirea obiectului ca “sortabil”.

Sortarea se invoca prin functia

template <class T>
tablou<T>& mergesort( tablou<T>& t ) {
  ( tmsort<T> )t;
  return t;
}

care consta in conversia tabloului t la tipul tmsort<T>. Clasa tmsort<T> incapsuleaza absolut toate detaliile sortarii. Fiind vorba de sortarea prin interclasare, detaliile de implementare sunt cele stabilite in Sectiunea 7.4.1.

template <class T>
class tmsort {
public:
  tmsort( tablou<T>& );

private:
  T *a;  // adresa zonei de sortat
  T *x;  // zona auxiliara de interclasare

  void mergesort( int, int );
};

Sortarea, de fapt transformarea tabloului t intr-un tablou sortat, este realizata prin constructorul

template <class T>
tmsort<T>::tmsort( tablou<T>& t ): a( t.a ) {
  x = new T[ t.size( ) ];    // alocarea zonei de interclasare
  mergesort( 0, t.size( ) ); // sortarea
  delete [ ] x;              // eliberarea zonei alocate
}

Dupa cum se observa, in acest constructor se foloseste membrul privat T *a (adresa zonei alocate elementelor tabloului) din clasa tablou<T>. Iata de ce, in clasa tablou<T> trebuie facuta o modificare (singura dealtfel): clasa tmsort<T> trebuie declarata friend.

Functia mergesort() este practic neschimbata:

template <class T>
void tmsort<T>::mergesort( int st, int dr ) {
  // ...
  // corpul functiei void mergesort( int, int, T* )
  // din Sectiunea 7.4.1.
  // ...
}

Pentru sortarea listelor se procedeaza analog, transformand implementarea din Sectiunea 7.4.1 in cea de mai jos.

template <class E>
lista<E>& mergesort( lista<E>& l ) {
  ( lmsort<E> )l;
  return l;
}

template <class E>
class lmsort {
public:
  lmsort( lista<E>& );

private:
  nod<E>* mergesort( nod<E>* );
  nod<E>* merge( nod<E>*, nod<E>* );
};

template <class E>
lmsort<E>::lmsort( lista<E>& l ) {
  if ( l.head )
    l.head = mergesort( l.head );
}

template <class E>
nod<E>* lmsort<E>::mergesort ( nod<E> *c ) {
  // ...
  // corpul functiei nod<E>* mergesort( nod<E>* )
  // din Sectiunea 7.4.1.
  // ...
}

template <class E>
nod<E>* lmsort<E>::merge( nod<E> *a, nod<E> *b ) {
  // ...
  // corpul functiei nod<E>* merge( nod<E>*, nod<E>* )
  // din Sectiunea 7.4.1.
  // ...
}

Nu uitati de declaratia friend! Clasa lmsort<E> foloseste membrii privati atat din clasa lista<E>, cat si din clasa nod<E>, deci trebuie declarata friend in ambele.

7.5 Quicksort (sortarea rapida)

Algoritmul de sortare quicksort, inventat de Hoare in 1962, se bazeaza de asemenea pe principiul divide et impera. Spre deosebire de mergesort, partea nerecursiva a algoritmului este dedicata construirii subcazurilor si nu combinarii solutiilor lor.

Ca prim pas, algoritmul alege un element pivot din tabloul care trebuie sortat. Tabloul este apoi partitionat in doua subtablouri, alcatuite de-o parte si de alta a acestui pivot in urmatorul mod: elementele mai mari decat pivotul sunt mutate in dreapta pivotului, iar celelalte elemente sunt mutate in stanga pivotului. Acest mod de partitionare este numit pivotare. In continuare, cele doua subtablouri sunt sortate in mod independent prin apeluri recursive ale algoritmului. Rezultatul este tabloul complet sortat; nu mai este necesara nici o interclasare. Pentru a echilibra marimea celor doua subtablouri care se obtin la fiecare partitionare, ar fi ideal sa alegem ca pivot elementul median. Intuitiv, mediana unui tablou T este elementul m din T, astfel incat numarul elementelor din T mai mici decat m este egal cu numarul celor mai mari decat m (o definitie riguroasa a medianei unui tablou este data in Sectiunea 7.6). Din pacate, gasirea medianei necesita mai mult timp decat merita. De aceea, putem pur si simplu sa folosim ca pivot primul element al tabloului. Iata cum arata acest algoritm:

procedure quicksort(T[i .. j])
     {sorteaza in ordine crescatoare tabloul T[i .. j]}
     if j-i este mic
          then  insert(T[i .. j])
          else   pivot(T[i .. j], l)
                   {dupa pivotare, avem:
                        i £ k < l   Þ   T[k] £ T[l]
                       l < k £ j   Þ   T[k] > T[l]}
                   quicksort(T[i .. l-1])
                   quicksort(T[l+1 .. j])

Mai ramane sa concepem un algoritm de pivotare cu timp liniar, care sa parcurga tabloul T o singura data. Putem folosi urmatoarea tehnica de pivotare: parcurgem tabloul T o singura data, pornind insa din ambele capete. Incercati sa intelegeti cum functioneaza acest algoritm de pivotare, in care p = T[i] este elementul pivot:

procedure pivot(T[i .. j], l)
     {permuta elementele din  T[i .. j] astfel incat, in final,
       elementele lui T[i .. l-1] sunt £ p,
       T[l] = p,
       iar elementele lui T[l+1 .. j] sunt > p}
     p ¬ T[i]
     k ¬ i; l ¬ j+1
     repeat    k ¬ k+1 until T[k] > p or k ³ j
     repeat    l ¬ l-1   until T[l] £ p
     while k < l do
          interschimba T[k] si T[l]
          repeat    k ¬ k+1 until T[k] > p
          repeat    l ¬ l-1   until T[l] £ p
     {pivotul este mutat in pozitia lui finala}
     interschimba T[i] si T[l]

Intuitiv, ne dam seama ca algoritmul quicksort este ineficient, daca se intampla in mod sistematic ca subcazurile T[i .. l-1] si T[l+1 .. j] sa fie puternic neechilibrate. Ne propunem in continuare sa analizam aceasta situatie in mod riguros.

Operatia de pivotare necesita un timp in Q(n). Fie constanta n₀, astfel incat, in cazul cel mai nefavorabil, timpul pentru a sorta n > n₀ elemente prin quicksort sa fie

t(n) Î Q(n) + max{t(i)+t(n-i-1) | 0 £ i £ n-1}

Folosim metoda inductiei constructive pentru a demonstra independent ca t Î O(n²) si t Î W(n²).

Putem considera ca exista o constanta reala pozitiva c, astfel incat t(i) £ ci²+c/2 pentru 0 £ i £ n₀. Prin ipoteza inductiei specificate partial, presupunem ca t(i) £ ci²+c/2 pentru orice 0 £ i < n. Demonstram ca proprietatea este adevarata si pentru n. Avem

t(n) £ dn + c + c max{i²+(n-i-1)² | 0 £ i £ n-1}

d fiind o alta constanta. Expresia i²+(n-i-1)² isi atinge maximul atunci cand i este 0 sau n-1. Deci,

t(n) £ dn + c + c(n-1)² = cn²+ c/2 + n(d-2c) + 3c/2

Daca luam c ³ 2d, obtinem t(n) £ cn²+c/2. Am aratat ca, daca c este suficient de mare, atunci t(n) £ cn²+c/2 pentru orice n ³ 0, adica, t Î O(n²). Analog se arata ca t Î W(n²).

Am aratat, totodata, care este cel mai nefavorabil caz: atunci cand, la fiecare nivel de recursivitate, procedura pivot este apelata o singura data. Daca elementele lui T sunt distincte, cazul cel mai nefavorabil este atunci cand initial tabloul este ordonat crescator sau descrescator, fiecare partitionare fiind total neechilibrata. Pentru acest cel mai nefavorabil caz, am aratat ca algoritmul quicksort necesita un timp in Q(n²).

Ce se intampla insa in cazul mediu? Intuim faptul ca, in acest caz, subcazurile sunt suficient de echilibrate. Pentru a demonstra aceasta proprietate, vom arata ca timpul necesar este in ordinul lui n log n, ca si in cazul cel mai favorabil.

Presupunem ca avem de sortat n elemente distincte si ca initial ele pot sa apara cu probabilitate egala in oricare din cele n! permutari posibile. Operatia de pivotare necesita un timp liniar. Apelarea procedurii pivot poate pozitiona primul element cu probabilitatea 1/n in oricare din cele n pozitii. Timpul mediu pentru quicksort verifica relatia

t(n) Î Q(n) + 1/n

Mai precis, fie n₀ si d doua constante astfel incat pentru orice n > n₀, avem

t(n) £ dn + 1/n

= dn + 2/n

Prin analogie cu mergesort, este rezonabil sa presupunem ca t Î O(n log n) si sa aplicam tehnica inductiei constructive, cautand o constanta c, astfel incat t(n) £ cn lg n.

Deoarece i lg i este o functie nedescrescatoare, avem

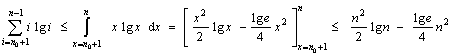
pentru n₀ ³ 1.

Tinand cont de aceasta margine superioara pentru

puteti demonstra prin inductie matematica ca t(n) £ cn lg n pentru orice n > n₀ ³ 1, unde

Rezulta ca timpul mediu pentru quicksort este in O(n log n). Pe langa ordinul timpului, un rol foarte important il are constanta multiplicativa. Practic, constanta multiplicativa pentru quicksort este mai mica decat pentru heapsort sau mergesort. Daca pentru cazul cel mai nefavorabil se accepta o executie ceva mai lenta, atunci, dintre tehnicile de sortare prezentate, quicksort este algoritmul preferabil.

Pentru a minimiza sansa unui timp de executie in W(n²), putem alege ca pivot mediana sirului T[i], T[(i+j) div 2], T[ j]. Pretul platit pentru aceasta modificare este o usoara crestere a constantei multiplicative.

7.6 Selectia unui element dintr-un tablou

Putem gasi cu usurinta elementul maxim sau minim al unui tablou T. Cum putem determina insa eficient mediana lui T ? Pentru inceput, sa definim formal mediana unui tablou.

Un element m al tabloului T[1 .. n] este mediana lui T, daca si numai daca sunt verificate urmatoarele doua relatii:

#{i Î {1, …, n} | T[i] < m} < én/2ù

#{i Î {1, …, n} | T[i] £ m} ³ én/2ù

Aceasta definitie tine cont de faptul ca n poate fi par sau impar si ca elementele din T pot sa nu fie distincte. Prima relatie este mai usor de inteles daca observam ca

#{i Î {1, …, n} | T[i] < m} = n - #{i Î {1, …, n} | T[i] ³ m}

Conditia

#{i Î {1, …, n} | T[i] < m} < én/2ù

este deci echivalenta cu conditia

#{i Î {1, …, n} | T[i] ³ m} > n - én/2ù = ën/2û

Algoritmul “naiv” pentru determinarea medianei lui T consta in a sorta crescator tabloul si a extrage apoi elementul din pozitia én/2ù. Folosind mergesort, de exemplu, acest algoritm necesita un timp in Q(n log n). Putem gasi o metoda mai eficienta? Pentru a raspunde la aceasta intrebare, vom considera o problema mai generala.

Fie T un tablou de n elemente si fie k un intreg, 1 £ k £ n. Problema selectiei consta in gasirea celui de-al k-lea cel mai mic element al lui T, adica a elementul m pentru care avem:

#{i Î {1, …, n} | T[i] < m} < k

#{i Î {1, …, n} | T[i] £ m} ³ k

Cu alte cuvinte, este al k-lea element in T, daca tabloul este sortat in ordine crescatoare. De exemplu, mediana lui T este al  én/2ù-lea cel mai mic element al lui T. Deoarece én/2ù = ë(n+1)/2û = (n+1) div 2, mediana lui T este totodata al ((n+1) div 2)-lea cel mai mic element al lui T.

Urmatorul algoritm, inca nu pe deplin specificat, rezolva problema selectiei intr-un mod similar cu quicksort dar si cu binsearch.

function selection(T[1 .. n], k)
     {gaseste al k-lea cel mai mic element al lui T;
       se presupune ca 1 £ k £ n}
     if n este mic then sorteaza T
                                 return T[k]
     p ¬ un element pivot din T[1 .. n]
     u ¬ #{i Î {1, …, n} | T[i] < p}
     v ¬ #{i Î {1, …, n} | T[i] £ p}
     if u ³ k then
          array U[1 .. u]
          U ¬ elementele din T mai mici decat p
          {cel de-al k-lea cel mai mic element al lui T este
            si cel de-al k-lea cel mai mic element al lui U}
          return selection (U, k)
     if v ³ k then {am gasit!} return p

     {situatia cand u < k si v < k}
     array V[1 .. n-v]
     V ¬ elementele din T mai mari decat p
     {cel de-al k-lea cel mai mic element al lui T este
       si cel de-al (k-v)-lea cel mai mic element al lui V}
     return selection(V, k-v)

Care element din T sa fie ales ca pivot? O alegere naturala este mediana lui T, astfel incat U si V sa fie de marimi cat mai apropiate (chiar daca cel mult unul din aceste subtablouri va fi folosit intr-un apel recursiv). Daca in algoritmul selection alegerea pivotului se face prin atribuirea

     p ¬ selection(T, (n+1) div 2)

ajungem insa la un cerc vicios.

Sa analizam algoritmul de mai sus, presupunand, pentru inceput, ca gasirea medianei este o operatie elementara. Din definitia medianei, rezulta ca u < én/2ù si v ³ én/2ù. Obtinem atunci relatia n-v £ ën/2û. Daca exista un apel recursiv, atunci tablourile U si V contin fiecare cel mult ën/2û elemente. Restul operatiilor necesita un timp in ordinul lui n. Fie t_m(n) timpul necesar acestei metode, in cazul cel mai nefavorabil, pentru a gasi al k-lea cel mai mic element al unui tablou de n elemente. Avem

t_m(n) Î O(n) + max{t_m(i) | i £ ën/2û}

De aici se deduce (Exercitiul 7.17) ca t_m Î O(n).

Ce facem insa daca trebuie sa tinem cont si de timpul pentru gasirea pivotului? Putem proceda ca in cazul quicksort-ului si sa renuntam la mediana, alegand ca pivot primul element al tabloului. Algoritmul selection astfel precizat are timpul pentru cazul mediu in ordinul exact al lui n. Pentru cazul cel mai nefavorabil, se obtine insa un timp in ordinul lui n².

Putem evita acest caz cel mai nefavorabil cu timp patratic, fara sa sacrificam comportarea liniara pentru cazul mediu. Ideea este sa gasim rapid o aproximare buna pentru mediana. Presupunand n ³ 5, vom determina pivotul prin atribuirea

     p ¬ pseudomed(T)

unde algoritmul pseudomed este:

function pseudomed(T[1 .. n])
     {gaseste o aproximare a medianei lui T}
     s ¬ n div 5
     array S[1 .. s]
     for i ¬ 1 to s do S[i] ¬ adhocmed5(T[5i-4 .. 5i])
     return selection(S, (s+1) div 2)

Algoritmul adhocmed5 este elaborat special pentru a gasi mediana a exact cinci elemente. Sa notam ca adhocmed5 necesita un timp in O(1).

Fie m aproximarea medianei tabloului T, gasita prin algoritmul pseudomed. Deoarece m este mediana tabloului S, avem

#{i Î {1, …, s} | S[i] £ m} ³ és/2ù

Fiecare element din S este mediana a cinci elemente din T. In consecinta, pentru fiecare i, astfel incat S[i] £ m, exista i₁, i₂, i₃ intre 5i-4 si 5i, astfel ca

T[i₁] £ T[i₂] £ T[i₃] = S[i] £ m

Deci,

#{i Î {1, …, n} | T[i] £ m} ³ 3és/2ù = 3éën/5û/2ù

= 3éé(n-4)/5ù/2ù = 3é(n-4)/10ù ³ (3n-12)/10

Similar, din relatia

#{i Î {1, …, s} | S[i] < m} < és/2ù

care este echivalenta cu

#{i Î {1, …, s} | S[i] ³ m} > ës/2û

deducem

#{i Î {1, …, n} | T[i] ³ m} > 3ëën/5ë/2û

= 3ën/10û = 3é(n-9)/10ù ³ (3n-27)/10

Deci,

#{i Î {1, …, n} | T[i] < m} < (7n+27)/10

In concluzie, m aproximeaza mediana lui T, fiind al k-lea cel mai mic element al lui T, unde k este aproximativ intre 3n/10 si 7n/10. O interpretare grafica ne va ajuta sa intelegem mai bine aceste relatii. Sa ne imaginam elementele lui T dispuse pe cinci linii, cu posibila exceptie a cel mult patru elemente (Figura 7.1). Presupunem ca fiecare din cele ën/5û coloane este ordonata nedescrescator, de sus in jos. De asemenea, presupunem ca linia din mijloc (corespunzatoare tabloului S din algoritm) este ordonata nedescrescator, de la stanga la dreapta. Elementul subliniat corespunde atunci medianei lui S, deci lui m. Elementele din interiorul dreptunghiului sunt mai mici sau egale cu m. Dreptunghiul contine aproximativ 3/5 din jumatatea elementelor lui T, deci in jur de 3n/10 elemente.

Presupunand ca folosim “p ¬ pseudomed(T)”, adica pivotul este pseudomediana, fie t(n) timpul necesar algoritmului selection, in cazul cel mai nefavorabil, pentru a gasi al k-lea cel mai mic element al unui tablou de n elemente. Din inegalitatile

#{i Î {1, …, n} | T[i] £ m} ³ (3n-12)/10

 #{i Î {1, …, n} | T[i] < m} < (7n+27)/10

rezulta ca, pentru n suficient de mare, tablourile U si V au cel mult 3n/4 elemente fiecare. Deducem relatia

t(n) Î O(n) + t(ën/5û) + max{t(i) | i £ 3n/4}                   (*)

Vom arata ca t Î Q(n). Sa consideram functia f : N ® R^*, definita prin recurenta

f(n) = f(ën/5û) + f(ë3n/4û) + n

pentru n Î N. Prin inductie constructiva, putem demonstra ca exista constanta reala pozitiva a astfel incat f(n) £ an pentru orice n Î N. Deci, f Î O(n). Pe de alta parte, exista constanta reala pozitiva c, astfel incat t(n) £ cf(n) pentru orice n Î N⁺. Este adevarata atunci si relatia t Î O(n). Deoarece orice algoritm care rezolva problema selectiei are timpul de executie in W(n), rezulta t Î W(n), deci, t Î Q(n).

Generalizand, vom incerca sa aproximam mediana nu numai prin impartire la cinci, ci prin impartire la un intreg q oarecare, 1 < q £ n. Din nou, pentru n suficient de mare, tablourile U si V au cel mult 3n/4 elemente fiecare. Relatia (*) devine

t(n) Î O(n) + t(ën/qû) + max{t(i) | i £ 3n/4}                 (**)

Daca 1/q + 3/4 < 1, adica daca numarul de elemente asupra carora opereaza cele doua apeluri recursive din (**) este in scadere, deducem, intr-un mod similar cu situatia cand q = 5, ca timpul este tot liniar. Deoarece pentru orice q ³ 5 inegalitatea precedenta este verificata, ramane deschisa problema alegerii unui q pentru care sa obtinem o constanta multiplicativa cat mai mica.

In particular, putem determina mediana unui tablou in timp liniar, atat pentru cazul mediu cat si pentru cazul cel mai nefavorabil. Fata de algoritmul “naiv”, al carui timp este in ordinul lui n log n, imbunatatirea este substantiala.

7.7 O problema de criptologie

Alice si Bob doresc sa comunice anumite secrete prin telefon. Convorbirea telefonica poate fi insa ascultata si de Eva. In prealabil, Alice si Bob nu au stabilit nici un protocol de codificare si pot face acum acest lucru doar prin telefon. Eva va asculta insa si ea modul de codificare. Problema este cum sa comunice Alice si Bob, astfel incat Eva sa nu poata descifra codul, cu toate ca va cunoaste si ea protocolul de codificare[**] .

Pentru inceput, Alice si Bob convin in mod deschis asupra unui intreg p cu cateva sute de cifre si asupra unui alt intreg g intre 2 si p-1. Securitatea secretului nu este compromisa prin faptul ca Eva afla aceste numere.

La pasul doi, Alice si Bob aleg la intimplare cate un intreg A, respectiv B, mai mici decat p, fara sa-si comunice aceste numere. Apoi, Alice calculeaza a = g^A mod p si transmite rezultatul lui Bob; similar, Bob transmite lui Alice valoarea b = g^B mod p. In final, Alice calculeaza x = b^A mod p, iar Bob calculeaza y = a^B mod p. Vor ajunge la acelasi rezultat, deoarece x = y = g^AB mod p. Aceasta valoare este deci cunoscuta de Alice si Bob, dar ramane necunoscuta lui Eva. Evident, nici Alice si nici Bob nu pot controla direct care va fi aceasta valoare. Deci ei nu pot folosi acest protocol pentru a schimba in mod direct un anumit mesaj. Valoarea rezultata poate fi insa cheia unui sistem criptografic conventional.

Interceptand convorbirea telefonica, Eva va putea cunoaste in final urmatoarele numere: p, q, a si b. Pentru a-l deduce pe x, ea trebuie sa gaseasca un intreg A', astfel incat a = g^A' mod p si sa procedeze apoi ca Alice pentru a-l calcula pe x' = b^A' mod p. Se poate arata (Exercitiul 7.21) ca x' = x, deci ca Eva poate calcula astfel corect secretul lui Alice si Bob.

Calcularea lui A' din p, g si a este cunoscuta ca problema logaritmului discret si poate fi realizata de urmatorul algoritm.

function dlog(g, a, p)
     A ¬ 0; k ¬ 1
     repeat
          A ¬ A+1
          k ¬ kg
     until (a = k mod p) or (A = p)
     return A

Daca logaritmul nu exista, functia dlog va returna valoarea p. De exemplu, nu exista un intreg A, astfel incat 3 = 2^A mod 7. Algoritmul de mai sus este insa extrem de ineficient. Daca p este un numar prim impar, atunci este nevoie in medie de p/2 repetari ale buclei repeat pentru a ajunge la solutie (presupunand ca aceasta exista). Daca pentru efecuarea unei bucle este necesara o microsecunda, atunci timpul de executie al algoritmului poate fi mai mare decat varsta Pamantului! Iar aceasta se intampla chiar si pentru un numar zecimal p cu doar 24 de cifre.

Cu toate ca exista si algoritmi mai rapizi pentru calcularea logaritmilor discreti, nici unul nu este suficient de eficient daca p este un numar prim cu cateva sute de cifre. Pe de alta parte, nu se cunoaste pana in prezent un alt mod de a-l obtine pe x din p, g, a si b, decat prin calcularea logaritmului discret.

Desigur, Alice si Bob trebuie sa poata calcula rapid exponentierile de forma a = g^A mod p, caci altfel ar fi si ei pusi in situatia Evei. Urmatorul algoritm pentru calcularea exponentierii nu este cu nimic mai subtil sau eficient decat cel pentru logaritmul discret.

function dexpo1(g, A, p)
     a ¬ 1
     for i ¬ 1 to A do a ¬ ag
     return a mod p

Faptul ca x y z mod p = ((x y mod p) z) mod p pentru orice x, y, z si p, ne permite sa evitam memorarea unor numere extrem de mari. Obtinem astfel o prima imbunatatire:

function dexpo2(g, A, p)
     a ¬ 1
     for i ¬ 1 to A do a ¬ ag mod p
     return a

Din fericire pentru Alice si Bob, exista un algoritm eficient pentru calcularea exponentierii si care foloseste reprezentarea binara a lui A. Sa consideram pentru inceput urmatorul exemplu

x²⁵ = (((x²x)² )² )²x

L-am obtinut deci pe x²⁵ prin doar doua inmultiri si patru ridicari la patrat. Daca in expresia

x²⁵ = (((x²x)²1)²1)²x

inlocuim fiecare x cu un 1 si fiecare 1 cu un 0, obtinem secventa 11001, adica reprezentarea binara a lui 25. Formula precedenta pentru x²⁵ are aceasta forma, deoarece x²⁵ = x²⁴x, x²⁴ = (x¹² )² etc. Rezulta un algoritm divide et impera in care se testeaza in mod recursiv daca exponentul curent este par sau impar.

function dexpo(g, A, p)
     if A = 0 then return 1
     if A este impar then   a ¬ dexpo(g, A-1, p)
                                      return (ag mod p)
                            else   a ¬ dexpo(g, A/2, p)
                                      return (aa mod p)

Fie h(A) numarul de inmultiri modulo p efectuate atunci cand se calculeaza dexpo(g, A, p), inclusiv ridicarea la patrat. Atunci,

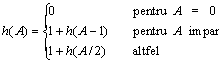
Daca M(p) este limita superioara a timpului necesar inmultirii modulo p a doua numere naturale mai mici decat p, atunci calcularea lui dexpo(g, A, p) necesita un timp in O(M(p) h(A)). Mai mult, se poate demonstra ca timpul este in O(M(p) log A), ceea ce este rezonabil. Ca si in cazul cautarii binare, algoritmul dexpo este mai curand un exemplu de simplificare decat de tehnica divide et impera.

Vom intelege mai bine acest algoritm, daca consideram si o versiune iterativa a lui.

function dexpoiter1(g, A, p)
     c ¬ 0; a ¬ 1
     {fie  reprezentarea binara a lui A}
     for i ¬ k downto 0 do
          c ¬ 2c
          a ¬ aa mod p
          if A_i = 1 then   c ¬ c + 1
                                 a ¬ ag mod p
     return a

Fiecare iteratie foloseste una din identitatile

g^2c mod p = (g^c )² mod p

g^2c+1 mod p = g(g^c )² mod p

in functie de valoarea lui A_i (daca este 0, respectiv 1). La sfarsitul pasului i, valoarea lui c, in reprezentare binara, este . Reprezentrea binara a lui A este parcursa de la stanga spre dreapta, invers ca la algoritmul dexpo. Variabila c a fost introdusa doar pentru a intelege mai bine cum functioneaza algoritmul si putem, desigur, sa o eliminam.

Daca parcurgem reprezentarea binara a lui A de la dreapta spre stanga, obtinem un alt algoritm iterativ la fel de interesant.

function dexpoiter2(g, A, p)
     n ¬ A; y ¬ g; a ¬ 1
     while n > 0 do
          if n este impar then a ¬ ay mod p
          y ¬ yy mod p
          n ¬ n div 2
     return a

Pentru a compara acesti trei algoritmi, vom considera urmatorul exemplu. Algoritmul dexpo il calculeaza pe x¹⁵ sub forma (((1 x)²x)²x)²x, cu sapte inmultiri; algoritmul dexpoiter1 sub forma (((1²x)²x)²x)²x, cu opt inmultiri; iar dexpoiter2 sub forma 1 x x²x⁴x⁸, tot cu opt inmultiri (ultima din acestea fiind pentru calcularea inutila a lui x¹⁶).

Se poate observa ca nici unul din acesti algoritmi nu minimizeaza numarul de inmultiri efectuate. De exemplu, x¹⁵ poate fi obtinut prin sase inmultiri, sub forma ((x²x)²x)²x. Mai mult, x¹⁵ poate fi obtinut prin doar cinci inmultiri (Exercitiul 7.22).

7.8 Inmultirea matricilor

Pentru matricile A si B de n ´ n elemente, dorim sa obtinem matricea produs C = AB. Algoritmul clasic provine direct din definitia inmultirii a doua matrici si necesita n³ inmultiri si (n-1)n² adunari scalare. Timpul necesar pentru calcularea matricii C este deci in Q(n³). Problema pe care ne-o punem este sa gasim un algoritm de inmultire matriciala al carui timp sa fie intr-un ordin mai mic decat n³. Pe de alta parte, este clar ca W(n²) este o limita inferioara pentru orice algoritm de inmultire matriciala, deoarece trebuie in mod necesar sa parcurgem cele n² elemente ale lui C.

Strategia divide et impera sugereaza un alt mod de calcul a matricii C. Vom presupune in continuare ca n este o putere a lui doi. Partitionam pe A si B in cate patru submatrici de n/2 ´ n/2 elemente fiecare. Matricea produs C se poate calcula conform formulei pentru produsul matricilor de 2 ´ 2 elemente:

unde

Pentru n = 2, inmultirile si adunarile din relatiile de mai sus sunt scalare; pentru n > 2, aceste operatii sunt intre matrici de n/2 ´ n/2 elemente. Operatia de adunare matriciala este cea clasica. In schimb, pentru fiecare inmultire matriciala, aplicam recursiv aceste partitionari, pana cand ajungem la submatrici de 2 ´ 2 elemente.

Pentru a obtine matricea C, este nevoie de opt inmultiri si patru adunari de matrici de n/2 ´ n/2 elemente. Doua matrici de n/2 ´ n/2 elemente se pot aduna intr-un timp in Q(n²). Timpul total pentru algoritmul divide et impera rezultat este

t(n) Î 8t(n/2) + Q(n²)

Definim functia

Din Proprietatea 5.2 rezulta ca f Î Q(n³). Procedand ca in Sectiunea 5.1.2, deducem ca t Î Q( f ) = Q(n³), ceea ce inseamna ca nu am castigat inca nimic fata de metoda clasica.

In timp ce inmultirea matricilor necesita un timp cubic, adunarea matricilor necesita doar un timp patratic. Este, deci, de dorit ca in formulele pentru calcularea submatricilor C sa folosim mai putine inmultiri, chiar daca prin aceasta marim numarul de adunari. Este insa acest lucru si posibil? Raspunsul este afirmativ. In 1969, Strassen a descoperit o metoda de calculare a submatricilor C_ij, care utilizeaza 7 inmultiri si 18 adunari si scaderi. Pentru inceput, se calculeaza sapte matrici de n/2 ´ n/2 elemente:

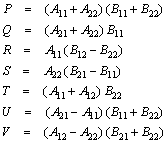
Este usor de verificat ca matricea produs C se obtine astfel:

Timpul total pentru noul algoritm divide et impera este

 t(n) Î 7t(n/2) + Q(n²)

si in mod similar deducem ca t Î Q(n^lg 7). Deoarece lg 7 < 2,81, rezulta ca t Î O(n^2,81). Algoritmul lui Strassen este deci mai eficient decat algoritmul clasic de inmultire matriciala.

Metoda lui Strassen nu este unica: s-a demonstrat ca exista exact 36 de moduri diferite de calcul a submatricilor C_ij, fiecare din aceste metode utilizand 7 inmultiri.

Limita O(n^2,81) poate fi si mai mult redusa daca gasim un algoritm de inmultire a matricilor de 2 ´ 2 elemente cu mai putin de sapte inmultiri. S-a demonstrat insa ca acest lucru nu este posibil. O alta metoda este de a gasi algoritmi mai eficienti pentru inmultirea matricilor de dimensiuni mai mari decat 2 ´ 2 si de a descompune recursiv pana la nivelul acestor submatrici. Datorita constantelor multiplicative implicate, exceptand algoritmul lui Strassen, nici unul din acesti algoritmi nu are o valoare practica semnificativa.

Pe calculator, s-a putut observa ca, pentru n ³ 40, algoritmul lui Strassen este mai eficient decat metoda clasica. In schimb, algoritmul lui Strassen foloseste memorie suplimentara.

Poate ca este momentul sa ne intrebam de unde provine acest interes pentru inmultirea matricilor. Importanta acestor algoritmi [***] deriva din faptul ca operatii frecvente cu matrici (cum ar fi inversarea sau calculul determinantului) se bazeaza pe inmultiri de matrici. Astfel, daca notam cu f (n) timpul necesar pentru a inmulti doua matrici de n ´ n elemente si cu g(n) timpul necesar pentru a inversa o matrice nesingulara de n ´ n elemente, se poate arata ca f Î Q(g).

7.9 Inmultirea numerelor intregi mari

Pentru anumite aplicatii, trebuie sa consideram numere intregi foarte mari. Daca ati implementat algoritmii pentru generarea numerelor lui Fibonacci, probabil ca v-ati confruntat deja cu aceasta problema. Acelasi lucru s-a intamplat in 1987, atunci cand s-au calculat primele 134 de milioane de cifre ale lui p. In criptologie, numerele intregi mari sunt de asemenea extrem de importante (am vazut acest lucru in Sectiunea 7.7). Operatiile aritmetice cu operanzi intregi foarte mari nu mai pot fi efectuate direct prin hardware, deci nu mai putem presupune, ca pana acum, ca operatiile necesita un timp constant. Reprezentarea operanzilor in virgula flotanta ar duce la aproximari nedorite. Suntem nevoiti deci sa implementam prin software operatiile aritmetice respective.

In cele ce urmeaza, vom da un algoritm divide et impera pentru inmultirea intregilor foarte mari. Fie u si v doi intregi foarte mari, fiecare de n cifre zecimale (convenim sa spunem ca un intreg k are j cifre daca k < 10 ^j, chiar daca k < 10 ^j-1). Daca s = ën/2û, reprezentam pe u si v astfel:

 u = 10^sw + x,    v = 10^sy + z,    unde  0 £ x < 10^s, 0 £ z < 10^s

Intregii w si y au cate én/2ù cifre, iar intregii x si z au cate ën/2û cifre. Din relatia

uv = 10^2swy + 10^s(wz+xy) + xz

obtinem urmatorul algoritm divide et impera pentru inmultirea a doua numere intregi mari.

function inmultire(u, v)
     n ¬ cel mai mic intreg astfel incat u si v sa aiba fiecare n cifre
     if n este mic then calculeaza in mod clasic produsul uv
                                 return produsul uv astfel calculat
     s ¬ n div 2
     w ¬ u div 10^s ;      x ¬ u mod 10^s
     y ¬ v div 10^s ;       z ¬ v mod 10^s
     return    inmultire(w, y) ´ 10^2s
                   + (inmultire(w, z)+inmultire(x, y)) ´ 10^s
                   + inmultire(x, z)

Presupunand ca folosim reprezentarea din Exercitiul 7.28, inmultirile sau impartirile cu 10^2s si 10^s, ca si adunarile, sunt executate intr-un timp liniar. Acelasi lucru este atunci adevarat si pentru restul impartirii intregi, deoarece

u mod 10^s = u - 10^sw,    v mod 10^s = v - 10^s y

Notam cu t_d (n) timpul necesar acestui algoritm, in cazul cel mai nefavorabil, pentru a inmulti doi intregi de n cifre. Avem

t_d (n) Î 3t_d (én/2ù) + t_d (ën/2û) + Q(n)

Daca n este o putere a lui 2, aceasta relatie devine

t_d (n) Î 4t_d (n/2) + Q(n)

Folosind Proprietatea 5.2, obtinem relatia t_d Î Q(n²). (Se observa ca am reintalnit un exemplu din Sectiunea 5.3.5). Inmultirea clasica necesita insa tot un timp patratic (Exercitiul 5.29). Nu am castigat astfel nimic; dimpotriva, am reusit sa marim constanta multiplicativa!

Ideea care ne va ajuta am mai folosit-o la metoda lui Strassen (Sectiunea 7.8). Deoarece inmultirea intregilor mari este mult mai lenta decat adunarea, incercam sa reducem numarul inmultirilor, chiar daca prin aceasta marim numarul adunarilor. Adica, incercam sa calculam wy, wz+xy si xz prin mai putin de patru inmultiri. Considerand produsul

r = (w+x)(y+z) = wy + (wz+xy) + xz

observam ca putem inlocui ultima linie din algoritm cu

r ¬ inmult(w+x, y+z)
p ¬ inmult(w, y); q ¬ inmult(x, z)
return 10^2sp + 10^s(r-p-q)  + q

Fie t(n) timpul necesar algoritmului modificat pentru a inmulti doi intregi, fiecare cu cel mult n cifre. Tinand cont ca w+x si y+z pot avea cel mult 1+én/2ù cifre, obtinem

t(n) Î t(ën/2û) + t(én/2ù) + t(1+én/2ù) + O(n)

Prin definitie, functia t este nedescrescatoare. Deci,

t(n) Î 3t(1+én/2ù) + O(n)

Notand T(n) = t(n+2) si presupunand ca n este o putere a lui 2, obtinem

T(n) Î 3T(n/2)  + O(n)

Prin metoda iteratiei (ca in Exercitiul 7.24), puteti arata ca

T Î O(n^lg 3 | n este o putere a lui 2)

Sau, mai elegant, puteti ajunge la acelasi rezultat aplicand o schimbare de variabila (o recurenta asemanatoare a fost discutata in Sectiunea 5.3.5). Deci,

t Î O(n^lg 3 | n este o putere a lui 2)

Tinand din nou cont ca t este nedescrescatoare, aplicam Proprietatea 5.1 si obtinem t Î O(n^lg 3).

In concluzie, este posibil sa inmultim doi intregi de n cifre intr-un timp in O(n^lg 3), deci si in O(n^1,59). Ca si la metoda lui Strassen, datorita constantelor multiplicative implicate, acest algoritm este interesant in practica doar pentru valori mari ale lui n. O implementare buna nu va folosi probabil baza 10, ci baza cea mai mare pentru care hardware-ul permite ca doua “cifre” sa fie inmultite direct.

7.10 Exercitii

7.1       Demonstrati ca procedura binsearch se termina intr-un numar finit de pasi (nu cicleaza).

Indicatie: Aratati ca binrec(T[i .. j], x) este apelata intotdeauna cu i £ j si ca binrec(T[i .. j], x) apeleaza binrec(T[u .. v], x) intotdeauna astfel incat

v-u < j-i

7.2       Se poate inlocui in algoritmul iterbin1:

i)     “k ¬ (i+j+1) div 2” cu “k ¬ (i+j) div 2”?
ii)    “i ¬ k” cu “i ¬ k+1”?
iii)  “j ¬ k-1” cu “j ¬ k”?

7.3       Observati ca bucla while din algoritmul insert (Sectiunea 1.3) foloseste o cautare secventiala (de la coada la cap). Sa inlocuim aceasta cautare secventiala cu o cautare binara. Pentru cazul cel mai nefavorabil, ajungem oare acum ca timpul pentru sortarea prin insertie sa fie in ordinul lui n log n?

7.4       Aratati ca timpul pentru iterbin2 este in Q(1), Q(log n), Q(log n) pentru cazurile cel mai favorabil, mediu si respectiv, cel mai nefavorabil.

7.5       Fie T[1 .. n] un tablou ordonat crescator de intregi diferiti, unii putand fi negativi. Dati un algoritm cu timpul in O(log n) pentru cazul cel mai nefavorabil, care gaseste un index i, 1 £ i £ n, cu T[i] = i, presupunand ca acest index exista.

7.6       Radacina patrata intreaga a lui n Î N este prin definitie acel p Î N pentru care p £   < p+1. Presupunand ca nu avem o functie radical, elaborati un algoritm care il gaseste pe p intr-un timp in O(log n).

Solutie: Se apeleaza patrat(0, n+1, n), patrat fiind functia

function patrat(a, b, n)
     if a = b-1 then return a
     m ¬ (a+b) div 2
     if m² £ n    then   patrat(m, b, n)
                     else   patrat(a, m, n)

7.7       Fie tablourile U[1 .. N] si V[1 .. M], ordonate crescator. Elaborati un algoritm cu timpul de executie in Q(N+M), care sa interclaseze cele doua tablouri. Rezultatul va fi trecut in tabloul T[1 .. N+M].

Solutie: Iata o prima varianta a acestui algoritm:

i, j, k ¬ 1
while i £ N and j £ M do
     if U[i] £ V[j]    then   T[k] ¬ U[i]
                                      i ¬ i+1
                            else   T[k] ¬ V[j]
                                      j ¬ j+1
     k ¬ k+1
if i > N   then for h ¬ j to M do
                   T[k] ¬ V[h]
                   k ¬ k+1
              else for h ¬ i to N do
                   T[k] ¬ U[h]
                   k ¬ k+1

Se poate obtine un algoritm si mai simplu, daca se presupune ca avem acces la locatiile U[N+1] si V[M+1], pe care le vom initializa cu o valoare maximala si le vom folosi ca “santinele”:

i, j ¬ 1
U[N+1], V[M+1] ¬ +¥
for k ¬ 1 to N+M do
     if U[i] < V[j]    then   T[k] ¬ U[i]
                                      i ¬ i+1
                            else   T[k] ¬ V[j]
                                      j ¬ j+1

Mai ramane sa analizati eficienta celor doi algoritmi.

7.8       Modificati algoritmul mergesort astfel incat T sa fie separat nu in doua, ci in trei parti de marimi cat mai apropiate. Analizati algoritmul obtinut.

7.9       Aratati ca, daca in algoritmul mergesort separam pe T in tabloul U, avand n-1 elemente, si tabloul V, avand un singur element, obtinem un algoritm de sortare cu timpul de executie in Q(n²). Acest nou algoritm seamana cu unul dintre algoritmii deja cunoscuti. Cu care anume?

7.10     Iata si o alta procedura de pivotare:

procedure pivot1(T[i .. j], l)
     p ¬ T[i]
     l ¬ i
     for k ¬ i+1 to j do
          if T[k] £ p  then   l ¬ l+1
                                      interschimba T[k] si T[l]
     interschimba T[i] si T[l]

Argumentati de ce procedura este corecta si analizati eficienta ei. Comparati numarul maxim de interschimbari din procedurile pivot si pivot1. Este oare rentabil ca in algoritmul quicksort sa inlocuim procedura pivot cu procedura pivot1?

7.11     Argumentati de ce un apel funny-sort(T[1 ..n ]) al urmatorului algoritm sorteaza corect elementele tabloului T[1 .. n].

procedure funny-sort(T[i .. j])
     if T[i] > T[ j] then interschimba T[i] si T[ j]
     if i < j-1 then  k ¬ ( j-i+1) div 3
                            funny-sort(T[i .. j-k])
                            funny-sort(T[i+k .. j])
                            funny-sort(T[i .. j-k])

Este oare acest simpatic algoritm si eficient?

7.12     Este un lucru elementar sa gasim un algoritm care determina minimul dintre elementele unui tablou  T[1 .. n] si utilizeaza pentru aceasta n-1 comparatii intre elemente ale tabloului. Mai mult, orice algoritm care determina prin comparatii minimul elementelor din T efectueaza in mod necesar cel putin n-1 comparatii. In anumite aplicatii, este nevoie sa gasim atat minimul cat si maximul dintr-o multime de n elemente. Iata un algoritm care determina minimul si maximul dintre elementele tabloului T[1 .. n]:

procedure fmaxmin1(T[1 .. n], max, min)
     max, min ¬ T[1]
     for i ¬ 2 to n do
          if max < T[i]  then max ¬ T[i]
          if min > T[i]         then min ¬ T[i]

Acest algoritm efectueaza 2(n-1) comparatii intre elemente ale lui T. Folosind tehnica divide et impera, elaborati un algoritm care sa determine minimul si maximul dintre elementele lui T prin mai putin de 2(n-1) comparatii. Puteti presupune ca n este o putere a lui 2.

Solutie: Un apel fmaxmin2(T[1 .. n], max, min) al urmatorului algoritm gaseste minimul si maximul cerute

procedure fmaxmin2(T[i .. j], max, min)
     case   i = j : max, min ¬ T[i]
              i = j-1 : if T[i] < T[ j]     then   max ¬ T[ j]
                                                              min ¬ T[i]
                                                    else   max ¬ T[i]
                                                              min ¬ T[ j]
              otherwise : m ¬ (i+j) div 2
                                 fmaxmin2(T[i .. m], smax, smin)
                                 fmaxmin2(T[m+1 .. j], dmax, dmin)
                                 max ¬ maxim(smax, dmax)
                                 min ¬ minim(smin, dmin)

Functiile maxim si minim determina, prin cate o singura comparatie, maximul, respectiv minimul, a doua elemente.

Putem deduce ca atat fmaxmin1, cat si fmaxmin2 necesita un timp in Q(n) pentru a gasi minimul si maximul intr-un tablou de n elemente. Constanta multiplicativa asociata timpului in cele doua cazuri difera insa. Notand cu C(n) numarul de comparatii intre elemente ale tabloului T efectuate de procedura fmaxmin2, obtinem recurenta

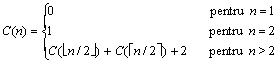
Consideram n = 2^k si folosim metoda iteratiei:

Algoritmul fmaxmin2 necesita cu 25% mai putine comparatii decat fmaxmin1. Se poate arata ca nici un algoritm bazat pe comparatii nu poate folosi mai putin de 3n/2-2 comparatii. In acest sens, fmaxmin2 este, deci, optim.

Este procedura fmaxmin2 mai eficienta si in practica? Nu in mod necesar. Analiza ar trebui sa considere si numarul de comparatii asupra indicilor de tablou, precum si timpul necesar pentru rezolvarea apelurilor recursive in fmaxmin2. De asemenea, ar trebui sa cunoastem si cu cat este mai costisitoare o comparatie de elemente ale lui T, decat o comparatie de indici (adica, de intregi).

7.13     In ce consta similaritatea algoritmului selection cu algoritmul i) quicksort si ii) binsearch?

7.14     Generalizati procedura pivot, partitionand tabloul T in trei sectiuni T[1 .. i-1], T[i .. j], T[ j+1 .. n], continand elementele lui T mai mici decat p, egale cu p si respectiv, mai mari decat p. Valorile i si j vor fi calculate in procedura de pivotare si vor fi returnate prin aceasta procedura.

7.15     Folosind ca model versiunea iterativa a cautarii binare si rezultatul Exercitiului 7.14, elaborati un algoritm nerecursiv pentru problema selectiei.

7.16     Analizati urmatoarea varianta a algoritmului quicksort.

procedure quicksort-modificat(T[1 .. n])
     if n = 2 and T[2] < T[1]
          then interschimba T[1] si T[2]
          else if n > 2 then
                   p ¬ selection(T, (n+1) div 2)
                   arrays U[1 .. (n+1) div 2 ], V[1 .. n div 2]
                   U ¬   elementele din T mai mici decat p
                            si, in completare, elemente egale cu p
                   V ¬   elementele din T mai mari decat p
                            si, in completare, elemente egale cu p
                   quicksort-modificat(U)
                   quicksort-modificat(V)

7.17     Daca presupunem ca gasirea medianei este o operatie elementara, am vazut ca timpul pentru selection, in cazul cel mai nefavorabil, este

t_m(n) Î O(n) + max{t_m (i) | i £ ën/2û}

Demonstrati ca t_m Î O(n).

Solutie: Fie n₀ si d doua constante astfel incat pentru n > n₀ avem

t_m (n) £ dn + max{t_m (i) | i £ ën/2û}

Putem considera ca exista constanta reala pozitiva c astfel incat t_m(i) £ ci+c, pentru 0 £ i £ n₀. Prin ipoteza inductiei specificate partial presupunem ca t(i) £ ci+c, pentru orice 0 £ i < n. Atunci

t_m(n) £ dn+c+cën/2û = cn+c+dn-cén/2ù £ cn+c

deoarece putem sa alegem constanta c suficient de mare, astfel incat cén/2ù ³ dn. Am aratat deci prin inductie ca, daca c este suficient de mare, atunci t_m(n) £ cn+c, pentru orice n ³ 0. Adica, t_m Î O(n).

7.18     Aratati ca luand “p ¬ T[1]” in algoritmul selection si considerand cazul cel mai nefavorabil, determinarea celui de-al k-lea cel mai mic element al lui T[1 .. n] necesita un timp de executie in O(n²).

7.19     Fie U[1 .. n] si V[1 .. n] doua tablouri de elemente ordonate nedescrescator. Elaborati un algoritm care sa gaseasca mediana celor 2n elemente intr-un timp de executie in O(log n).

7.20     Un element x este majoritar in tabloul T[1 .. n], daca #{i | T[i] = x} > ën/2û. Elaborati un algoritm liniar care sa determine elementul majoritar in T (daca un astfel de element exista).

7.21     Sa presupunem ca Eva a gasit un A' pentru care

a = g^A' mod p = g^A mod p

si ca exista un B, astfel incat b = g^B mod p. Aratati ca

x' = b^A' mod p = b^A mod p = x

chiar daca A' ¹ A.

7.22     Aratati cum poate fi calculat x¹⁵ prin doar cinci inmultiri (inclusiv ridicari la patrat).

Solutie: x¹⁵ = (((x² )² )² )²x^-1

7.23     Gasiti un algoritm divide et impera pentru a calcula un termen oarecare din sirul lui Fibonacci. Folositi proprietatea din Exercitiul 1.7. Va ajuta aceasta la intelegerea algoritmului fib3 din Sectiunea 1.6.4?

Indicatie: Din Exercitiul 1.7, deducem ca f_n =  , unde  este elementul de pe ultima linie si ultima coloana ale matricii M ^n-1. Ramane sa elaborati un algoritm similar cu dexpo pentru a afla matricea putere M ^n-1. Daca, in loc de dexpo, folositi ca model algoritmul dexpoiter2, obtineti algoritmul fib3.

7.24     Demonstrati ca algoritmul lui Strassen necesita un timp in O(n^lg 7), folosind de aceasta data metoda iteratiei.

Solutie: Fie doua constante pozitive a si c, astfel incat timpul pentru algoritmul lui Strassen este

t(n) £ 7t(n/2) + cn²

pentru n > 2, iar t(n) £ a pentru n £ 2. Obtinem

          t(n) £   cn²(1+7/4+(7/4)²+…+(7/4)^k-2) + a7^k-1

                 £   cn²(7/4)^lg n + a7^lg n

                 =   cn^{lg 4+lg 7-lg 4} + an^lg 7 Î O(n^lg 7)

7.25     Cum ati modifica algoritmul lui Strassen pentru a inmulti matrici de n ´ n elemente, unde n nu este o putere a lui doi? Aratati ca timpul algoritmului rezultat este tot in Q(n^lg 7).

Indicatie: Il majoram pe n pana la cea mai mica putere a lui 2, completand corespunzator matricile A si B cu elemente nule.

7.26     Sa presupunem ca avem o primitiva grafica box(x, y, r), care deseneaza un patrat 2r ´ 2r centrat in (x, y), stergand zona din interior. Care este desenul realizat prin apelul star(a, b, c), unde star este algoritmul

procedure star(x, y, r)
     if r > 0 then  star(x-r, y+r, r div 2)
                          star(x+r, y+r, r div 2)
                          star(x-r, y-r, r div 2)
                          star(x+r, y-r, r div 2)
                          box(x, y, r)

Care este rezultatul, daca box(x, y, r) apare inaintea celor patru apeluri recursive? Aratati ca timpul de executie pentru un apel star(a, b, c) este in Q(c²).

7.27     Demonstrati ca pentru orice intregi m si n sunt adevarate urmatoarele proprietati:

i)     daca m si n sunt pare, atunci cmmdc(m, n) = 2cmmdc(m/2, n/2)
ii)    daca m este impar si n este par, atunci cmmdc(m, n) = cmmdc(m, n/2)
iii)  daca m si n sunt impare, atunci cmmdc(m, n) = cmmdc((m-n)/2, n)

Pe majoritatea calculatoarelor, operatiile de scadere, testare a paritatii unui intreg si impartire la doi sunt mai rapide decat calcularea restului impartirii intregi. Elaborati un algoritm divide et impera pentru a calcula cel mai mare divizor comun a doi intregi, evitand calcularea restului impartirii intregi. Folositi proprietatile de mai sus.

7.28     Gasiti o structura de date adecvata, pentru a reprezenta numere intregi mari pe calculator. Pentru un intreg cu n cifre zecimale, numarul de biti folositi trebuie sa fie in ordinul lui n. Inmultirea si impartirea cu o putere pozitiva a lui 10 (sau alta baza, daca preferati) trebuie sa poata fi efectuate intr-un timp liniar. Adunarea si scaderea a doua numere de n, respectiv m cifre trebuie sa poata fi efectuate intr-un timp in Q(n+m). Permiteti numerelor sa fie si negative.

7.29     Fie u si v doi intregi mari cu n, respectiv m cifre. Presupunand ca folositi structura de date din Exercitiul 7.28, aratati ca algoritmul de inmultire clasica (si cel “a la russe”) a lui u cu v necesita un timp in Q(nm).

[*]   Spatiul suplimentar utilizat de algoritmul mergesort poate fi independent de numarul elementelor tabloului de sortat. Detaliile de implementare a unei astfel de strategii se gasesc in D. E. Knuth, “Tratat de programarea calculatoarelor. Sortare si cautare”, Sectiunea 5.2.4.

[**]    O prima solutie a acestei probleme a fost data in 1976 de W. Diffie si M. E. Hellman. Intre timp s-au mai propus si alte protocoale.

[***]   S-au propus si metode complet diferite. Astfel, D. Coppersmith si S. Winograd au gasit  in 1987 un algoritm cu timpul in O(n^2,376).