6. Algoritmi greedy
  6.1 Tehnica greedy
  6.2 Minimizarea timpului mediu de asteptare
  6.3 Interclasarea optima a sirurilor ordonate
  6.4 Implementarea arborilor de interclasare
  6.5 Coduri Huffman
  6.6 Arbori partiali de cost minim
    6.6.1 Algoritmul lui Kruskal
    6.6.2 Algoritmul lui Prim
  6.7 Implementarea algoritmului lui Kruskal
  6.8 Cele mai scurte drumuri care pleaca din acelasi punct
  6.9 Implementarea algoritmului lui Dijkstra
  6.10 Euristica greedy
    6.10.1 Colorarea unui graf
    6.10.2 Problema comis-voiajorului
  6.11 Exercitii

6. Algoritmi greedy

Pusi in fata unei probleme pentru care trebuie sa elaboram un algoritm, de multe ori “nu stim cum sa incepem”. Ca si in orice alta activitate, exista cateva principii generale care ne pot ajuta in aceasta situatie. Ne propunem sa prezentam in urmatoarele capitole tehnicile fundamentale de elaborare a algoritmilor. Cateva din aceste metode sunt atat de generale, incat le folosim frecvent, chiar daca numai intuitiv, ca reguli elementare in gandire.

6.1 Tehnica greedy

Algoritmii greedy (greedy = lacom) sunt in general simpli si sunt folositi la probleme de optimizare, cum ar fi: sa se gaseasca cea mai buna ordine de executare a unor lucrari pe calculator, sa se gaseasca cel mai scurt drum intr-un graf etc. In cele mai multe situatii de acest fel avem:

·    o multime de candidati (lucrari de executat, varfuri ale grafului etc)
·    o functie care verifica daca o anumita multime de candidati constituie o solutie posibila, nu neaparat optima, a problemei
·    o functie care verifica daca o multime de candidati este fezabila, adica daca este posibil sa completam aceasta multime astfel incat sa obtinem o solutie posibila, nu neaparat optima, a problemei
·    o functie de selectie care indica la orice moment care este cel mai promitator dintre candidatii inca nefolositi
·    o functie obiectiv care da valoarea unei solutii (timpul necesar executarii tuturor lucrarilor intr-o anumita ordine, lungimea drumului pe care l-am gasit etc); aceasta este functia pe care urmarim sa o optimizam (minimizam/maximizam)

Pentru a rezolva problema noastra de optimizare, cautam o solutie posibila care sa optimizeze valoarea functiei obiectiv. Un algoritm greedy construieste solutia pas cu pas. Initial, multimea candidatilor selectati este vida. La fiecare pas, incercam sa adaugam acestei multimi cel mai promitator candidat, conform functiei de selectie. Daca, dupa o astfel de adaugare, multimea de candidati selectati nu mai este fezabila, eliminam ultimul candidat adaugat; acesta nu va mai fi niciodata considerat. Daca, dupa adaugare, multimea de candidati selectati este fezabila, ultimul candidat adaugat va ramane de acum incolo in ea. De fiecare data cand largim multimea candidatilor selectati, verificam daca aceasta multime nu constituie o solutie posibila a problemei noastre. Daca algoritmul greedy functioneaza corect, prima solutie gasita va fi totodata o solutie optima a problemei. Solutia optima nu este in mod necesar unica: se poate ca functia obiectiv sa aiba aceeasi valoare optima pentru mai multe solutii posibile. Descrierea formala a unui algoritm greedy general este:

 function greedy(C)
     {C este multimea candidatilor}
     S ¬ Æ    {S este multimea in care construim solutia}
     while not solutie(S) and C ¹ Æ do
          x ¬ un element din C care maximizeaza/minimizeaza select(x)
          C ¬ C \ {x}
          if fezabil(S È {x}) then S ¬ S È {x}
     if  solutie(S)        then   return S
                            else   return “nu exista solutie”

Este de inteles acum de ce un astfel de algoritm se numeste “lacom” (am putea sa-i spunem si “nechibzuit”). La fiecare pas, procedura alege cel mai bun candidat la momentul respectiv, fara sa-i pese de viitor si fara sa se razgandeasca. Daca un candidat este inclus in solutie, el ramane acolo; daca un candidat este exclus din solutie, el nu va mai fi niciodata reconsiderat. Asemenea unui intreprinzator rudimentar care urmareste castigul imediat in dauna celui de perspectiva, un algoritm greedy actioneaza simplist. Totusi, ca si in afaceri, o astfel de metoda poate da rezultate foarte bune tocmai datorita simplitatii ei.

Functia select este de obicei derivata din functia obiectiv; uneori aceste doua functii sunt chiar identice.

Un exemplu simplu de algoritm greedy este algoritmul folosit pentru rezolvarea urmatoarei probleme. Sa presupunem ca dorim sa dam restul unui client, folosind un numar cat mai mic de monezi. In acest caz, elementele problemei sunt:

·    candidatii: multimea initiala de monezi de 1, 5, si 25 unitati, in care presupunem ca din fiecare tip de moneda avem o cantitate nelimitata
·    o solutie posibila: valoarea totala a unei astfel de multimi de monezi selectate trebuie sa fie exact valoarea pe care trebuie sa o dam ca rest
·    o multime fezabila: valoarea totala a unei astfel de multimi de monezi selectate nu este mai mare decat valoarea pe care trebuie sa o dam ca rest
·    functia de selectie: se alege cea mai mare moneda din multimea de candidati ramasa
·    functia obiectiv: numarul de monezi folosite in solutie; se doreste minimizarea acestui numar

Se poate demonstra ca algoritmul greedy va gasi in acest caz mereu solutia optima (restul cu un numar minim de monezi). Pe de alta parte, presupunand ca exista si monezi de 12 unitati sau ca unele din tipurile de monezi lipsesc din multimea initiala de candidati, se pot gasi contraexemple pentru care algoritmul nu gaseste solutia optima, sau nu gaseste nici o solutie cu toate ca exista solutie.

Evident, solutia optima se poate gasi incercand toate combinarile posibile de monezi. Acest mod de lucru necesita insa foarte mult timp.

Un algoritm greedy nu duce deci intotdeauna la solutia optima, sau la o solutie. Este doar un principiu general, urmand ca pentru fiecare caz in parte sa determinam daca obtinem sau nu solutia optima.

6.2 Minimizarea timpului mediu de asteptare

O singura statie de servire (procesor, pompa de benzina etc) trebuie sa satisfaca cererile a n clienti. Timpul de servire necesar fiecarui client este cunoscut in prealabil: pentru clientul i este necesar un timp t_i, 1 £ i £ n. Dorim sa minimizam timpul total de asteptare

(timpul de asteptare pentru clientul i)

ceea ce este acelasi lucru cu a minimiza timpul mediu de asteptare, care este T/n. De exemplu, daca avem trei clienti cu t₁ = 5, t₂ = 10, t₃ = 3, sunt posibile sase ordini de servire. In primul caz, clientul 1 este servit primul, clientul 2 asteapta pana este servit clientul 1 si apoi este servit, clientul 3 asteapta pana sunt serviti clientii 1, 2 si apoi este servit. Timpul total de asteptare a celor trei clienti este 38.

Algoritmul greedy este foarte simplu: la fiecare pas se selecteaza clientul cu timpul minim de servire din multimea de clienti ramasa. Vom demonstra ca acest algoritm este optim. Fie

I = (i₁  i₂ ... i_n)

o permutare oarecare a intregilor {1, 2, ..., n}. Daca servirea are loc in ordinea I, avem

Presupunem acum ca I este astfel incat putem gasi doi intregi a < b cu

Interschimbam pe i_a cu i_b in I; cu alte cuvinte, clientul care a fost servit al b-lea va fi servit acum al a-lea si invers. Obtinem o noua ordine de servire J, care este de preferat deoarece

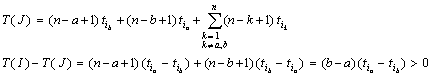
Prin metoda greedy obtinem deci intotdeauna planificarea optima a clientilor.

Problema poate fi generalizata pentru un sistem cu mai multe statii de servire.

6.3 Interclasarea optima a sirurilor ordonate

Sa presupunem ca avem doua siruri S₁ si S₂ ordonate crescator si ca dorim sa obtinem prin interclasarea lor sirul ordonat crescator care contine elementele din cele doua siruri. Daca interclasarea are loc prin deplasarea elementelor din cele doua siruri in noul sir rezultat, atunci numarul deplasarilor este #S₁ + #S₂.

Generalizand, sa consideram acum n siruri S₁, S₂, ..., S_n, fiecare sir S_i, 1 £ i £ n, fiind format din q_i elemente ordonate crescator (vom numi q_i lungimea lui S_i). Ne propunem sa obtinem sirul S ordonat crescator, continand exact elementele din cele n siruri. Vom realiza acest lucru prin interclasari succesive de cate doua siruri. Problema consta in determinarea ordinii optime in care trebuie efectuate aceste interclasari, astfel incat numarul total al deplasarilor sa fie cat mai mic. Exemplul de mai jos ne arata ca problema astfel formulata nu este banala, adica nu este indiferent in ce ordine se fac interclasarile.

Fie sirurile S₁, S₂, S₃ de lungimi q₁ = 30, q₂ = 20, q₃ = 10. Daca interclasam pe S₁ cu S₂, iar rezultatul il interclasam cu S₃, numarul total al deplasarilor este (30+20)+(50+10) = 110. Daca il interclasam pe S₃ cu S₂, iar rezultatul il interclasam cu S₁, numarul total al deplasarilor este (10+20)+(30+30) = 90.

Atasam fiecarei strategii de interclasare cate un arbore binar in care valoarea fiecarui varf este data de lungimea sirului pe care il reprezinta. Daca sirurile S₁, S₂, ..., S₆ au lungimile q₁ = 30, q₂ = 10, q₃ = 20, q₄ = 30, q₅ = 50, q₆ = 10, doua astfel de strategii de interclasare sunt reprezentate prin arborii din Figura 6.1.

Observam ca fiecare arbore are 6 varfuri terminale, corespunzand celor 6 siruri initiale si 5 varfuri neterminale, corespunzand celor 5 interclasari care definesc strategia respectiva. Numerotam varfurile in felul urmator: varful terminal i, 1 £ i £ 6, va corespunde sirului S_i, iar varfurile neterminale se numeroteaza de la 7 la 11 in ordinea obtinerii interclasarilor respective (Figura 6.2).

Strategia greedy apare in Figura 6.1b si consta in a interclasa mereu cele mai scurte doua siruri disponibile la momentul respectiv.

Interclasand sirurile S₁, S₂, ..., S_n, de lungimi q₁, q₂, ..., q_n, obtinem pentru fiecare strategie cate un arbore binar cu n varfuri terminale, numerotate de la 1 la n, si n–1 varfuri neterminale, numerotate de la n+1 la 2n–1. Definim, pentru un arbore oarecare A de acest tip, lungimea externa ponderata:

unde a_i este adancimea varfului i. Se observa ca numarul total de deplasari de elemente pentru strategia corespunzatoare lui A este chiar L(A). Solutia optima a problemei noastre este atunci arborele (strategia) pentru care lungimea externa ponderata este minima.

Proprietatea 6.1 Prin metoda greedy se obtine intotdeauna interclasarea optima a n siruri ordonate, deci strategia cu arborele de lungime externa ponderata minima.

Demonstratie: Demonstram prin inductie. Pentru n = 1, proprietatea este verificata. Presupunem ca proprietatea este adevarata pentru n–1 siruri. Fie A arborele strategiei greedy de interclasare a n siruri de lungime q₁ £ q₂ £ ... q_n. Fie B un arbore cu lungimea externa ponderata minima, corespunzator unei strategii optime de interclasare a celor n siruri. In arborele A apare subarborele

reprezentand prima interclasare facuta conform strategiei greedy. In arborele B, fie un varf neterminal de adancime maxima. Cei doi fii ai acestui varf sunt atunci doua varfuri terminale q_j si q_k. Fie B' arborele obtinut din B schimband intre ele varfurile q₁ si q_j, respectiv q₂ si q_k. Evident, L(B') £ L(B). Deoarece B are lungimea externa ponderata minima, rezulta ca L(B') = L(B). Eliminand din B' varfurile q₁ si q₂, obtinem un arbore B" cu n–1 varfuri terminale q₁+q₂, q₃, ..., q_n. Arborele B' are lungimea externa ponderata minima si L(B') = L(B") + (q₁+q₂). Rezulta ca si B" are lungimea externa ponderata minima. Atunci, conform ipotezei inductiei, avem L(B") = L(A'), unde A' este arborele strategiei greedy de interclasare a sirurilor de lungime q₁+q₂, q₃, ..., q_n. Cum A se obtine din A' atasand la varful q₁+q₂ fiii q₁ si q₂, iar B' se obtine in acelasi mod din B", rezulta ca L(A) = L(B') = L(B). Proprietatea este deci adevarata pentru orice n.

La scrierea algoritmului care genereaza arborele strategiei greedy de interclasare vom folosi un min-heap. Fiecare element al min-heap-ului este o pereche (q, i) unde i este numarul unui varf din arborele strategiei de interclasare, iar q este lungimea sirului pe care il reprezinta. Proprietatea de min-heap se refera la valoarea lui q.

Algoritmul interopt va construi arborele strategiei greedy. Un varf i al arborelui va fi memorat in trei locatii diferite continand:

                            LU[i]    =   lungimea sirului reprezentat de varf
                            ST[i]    =   numarul fiului stang
                            DR[i]    =   numarul fiului drept

 procedure interopt(Q[1 .. n])
     {construieste arborele strategiei greedy de interclasare
       a sirurilor de lungimi Q[i] = q_i, 1 £ i £ n}
     H ¬ min-heap vid
     for i ¬ 1 to n do
          (Q[i], i) Þ H        {insereaza in min-heap}
          LU[i] ¬ Q[i]; ST[i] ¬ 0; DR[i] ¬ 0
     for i ¬ n+1 to 2n–1 do
          (s, j)  Ü H       {extrage radacina lui H}
          (r, k) Ü H       {extrage radacina lui H}
          ST[i] ¬ j; DR[i] ¬ k; LU[i] ¬ s+r
          (LU[i], i) Þ H      {insereaza in min-heap}

In cazul cel mai nefavorabil, operatiile de inserare in min-heap si de extragere din min-heap necesita un timp in ordinul lui log n (revedeti Exercitiul 5.27). Restul operatiilor necesita un timp constant. Timpul total pentru interopt este deci in O(n log n).

6.4 Implementarea arborilor de interclasare

Transpunerea procedurii interopt intr-un limbaj de programare prezinta o singura dificultate generata de utilizarea unui min-heap de perechi varf-lungime. In limbajul C++, implementarea arborilor de interclasare este aproape o operatie de rutina, deoarece clasa parametrica heap (Sectiunea 4.2.2) permite manipularea unor heap-uri cu elemente de orice tip in care este definit operatorul de comparare >. Altfel spus, nu avem decat sa construim o clasa formata din perechi varf-lungime (pondere) si sa o completam cu operatorul > corespunzator. Vom numi aceasta clasa vp, adica varf-pondere.

#ifndef __VP_H
#define __VP_H

#include <iostream.h>

class vp {
public:
  vp( int vf = 0, float pd = 0 ) { v = vf; p = pd; }

  operator int  ( ) const { return v; }
  operator float( ) const { return p; }

  int v; float p;
};

inline operator > ( const vp& a, const vp& b) {
  return a.p <  b.p;
}

inline istream& operator >>( istream& is, vp& element ) {
  is >> element.v >> element.p; element.v--;
  return is;
}

inline ostream& operator <<( ostream& os, vp& element ) {
  os << "{ " << (element.v+1) << "; " << element.p << " }";
  return os;
}
#endif

Scopul clasei vp (definita in fisierul vp.h) nu este de a introduce un nou tip de date, ci mai curand de a facilita manipularea structurii varf-pondere, structura utila si la reprezentarea grafurilor. Din acest motiv, nu exista nici un fel de incapsulare, toti membrii fiind publici. Pentru o mai mare comoditate in utilizare, am inclus in definitie cei doi operatori de conversie, la int, respectiv la float, precum si operatorii de intrare/iesire.

Nu ne mai ramane decat sa precizam structura arborelui de interclasare. Cel mai simplu este sa preluam structura folosita in procedura interopt din Sectiunea 6.3: arborele este format din trei tablouri paralele, care contin lungimea sirului reprezentat de varful respectiv si indicii celor doi fii. Pentru o scriere mai compacta, vom folosi totusi o structura putin diferita: un tablou de elemente de tip nod, fiecare nod continand trei campuri corespunzatoare informatiilor de mai sus. Clasa nod este similara clasei vp, atat ca structura, cat si prin motivatia introducerii ei.

class nod {
public:
  int lu; // lungimea
  int st; // fiul stang
  int dr; // fiul drept
};

inline ostream& operator <<( ostream& os, nod& nd ) {
  os << " <" << nd.st << "< "
     << nd.lu
     << " >" << nd.dr << "> ";
  return os;
}

In limbajul C++, functia de construire a arborelui strategiei greedy se obtine direct, prin transcrierea procedurii interopt.

tablou<nod> interopt( const tablou<int>& Q ) {
  int n = Q.size( );

  tablou<nod> A( 2 * n - 1 ); // arborele de interclasare
  heap  <vp>  H( 2 * n - 1 );

  for ( int i = 0; i < n; i++ ) {
    H.insert( vp(i, Q[i]) );
    A[i].lu = Q[i]; A[i].st = A[i].dr = -1;
  }
  for ( i = n; i < 2 * n - 1; i++ ) {
    vp s; H.delete_max( s );
    vp r; H.delete_max( r );
    A[i].st = s; A[i].dr = r;
    A[i].lu = (float)s + (float)r;
    H.insert( vp(i, A[i].lu) );
  }

return A;
}

Functia de mai sus contine doua aspecte interesante:

·    Constructorul vp(int, float) este invocat explicit in functia de inserare in heap-ul H. Efectul acestei invocari consta in crearea unui obiect temporar de tip vp, obiect distrus dupa inserare. O notatie foarte simpla ascunde deci si o anumita ineficienta, datorata crearii si distrugerii obiectului temporar.
·    Operatorul de conversie la int este invocat implicit in expresiile A[i].st = s si A[i].dr = r, iar in expresia A[i].lu = (float)s + (float)r, operatorul de conversie la float trebuie sa fie specificat explicit. Semantica limbajului C++ este foarte clara relativ la conversii: cele utilizator au prioritate fata de cele standard, iar ambiguitatea in selectarea conversiilor posibile este semnalata ca eroare. Daca in primele doua atribuiri conversia lui s si r la int este singura posibilitate, scrierea celei de-a treia sub forma A[i].lu = s + r este ambigua, expresia s + r putand fi evaluata atat ca int cat si ca float.

In final, nu ne mai ramane decat sa testam functia interopt(). Vom folosi un tablou l cu lungimi de siruri, lungimi extrase din stream-ul standard de intrare.

main( ) {
  tablou<int> l;
  cout << "Siruri: "; cin >> l;
  cout << "Arborele de interclasare: ";
  cout << interopt( l ) << '\n';
  return 1;
}

Strategia de interclasare optima pentru cele sase lungimi folosite ca exemplu in Sectiunea6.3:

[ 6 ] 30 10 20 30 50 10

 este:

Arborele de interclasare:  [11]:  <-1< 30 >-1>  <-1< 10 >-1>
<-1< 20 >-1>   <-1< 30 >-1>   <-1< 50 >-1>   <-1< 10 >-1>
<1< 20 >5>   <2< 40 >6>   <3< 60 >0>   <7< 90 >4>
<8< 150 >9>

Valoarea fiecarui nod este precedata de indicele fiului stang si urmata de cel al fiului drept, indicele -1 reprezentand legatura inexistenta. Formatele de citire si scriere ale tablourilor sunt cele stabilite in Sectiunea 4.1.3.

6.5 Coduri Huffman

O alta aplicatie a strategiei greedy si a arborilor binari cu lungime externa ponderata minima este obtinerea unei codificari cat mai compacte a unui text.

Un principiu general de codificare a unui sir de caractere este urmatorul: se masoara frecventa de aparitie a diferitelor caractere dintr-un esantion de text si se atribuie cele mai scurte coduri, celor mai frecvente caractere, si cele mai lungi coduri, celor mai putin frecvente caractere. Acest principiu sta, de exemplu, la baza codului Morse. Pentru situatia in care codificarea este binara, exista o metoda eleganta pentru a obtine codul respectiv. Aceasta metoda, descoperita de Huffman (1952) foloseste o strategie greedy si se numeste codificarea Huffman. O vom descrie pe baza unui exemplu.

Fie un text compus din urmatoarele litere (in paranteze figureaza frecventele lor de aparitie):

S (10), I (29), P (4), O (9), T (5)

Conform metodei greedy, construim un arbore binar fuzionand cele doua litere cu frecventele cele mai mici. Valoarea fiecarui varf este data de frecventa pe care o reprezinta.

Etichetam muchia stanga cu 1 si muchia dreapta cu 0. Rearanjam tabelul de frecvente:

S (10), I (29), O (9), {P, T} (4+5 = 9)

Multimea {P, T} semnifica evenimentul reuniune a celor doua evenimente independente corespunzatoare aparitiei literelor P si T. Continuam procesul, obtinand arborele

In final, ajungem la arborele din Figura 6.3, in care fiecare varf terminal corespunde unei litere din text.

Pentru a obtine codificarea binara a literei P, nu avem decat sa scriem secventa de 0-uri si 1-uri in ordinea aparitiei lor pe drumul de la radacina catre varful corespunzator lui P: 1011. Procedam similar si pentru restul literelor:

 S (11), I (0), P (1011), O (100), T (1010)

Pentru un text format din n litere care apar cu frecventele f₁, f₂, ..., f_n, un arbore de codificare este un arbore binar cu varfurile terminale avand valorile f₁, f₂, ..., f_n, prin care se obtine o codificare binara a textului. Un arbore de codificare nu trebuie in mod necesar sa fie construit dupa metoda greedy a lui Huffman, alegerea varfurilor care sunt fuzionate la fiecare pas putandu-se face dupa diverse criterii. Lungimea externa ponderata a unui arbore de codificare este:

unde a_i este adincimea varfului terminal corespunzator literei i. Se observa ca lungimea externa ponderata este egala cu numarul total de caractere din codificarea textului considerat. Codificarea cea mai compacta a unui text corespunde deci arborelui de codificare de lungime externa ponderata minima. Se poate demonstra ca arborele de codificare Huffman minimizeaza lungimea externa ponderata pentru toti arborii de codificare cu varfurile terminale avand valorile f₁, f₂, ..., f_n. Prin strategia greedy se obtine deci intotdeauna codificarea binara cea mai compacta a unui text.

Arborii de codificare pe care i-am considerat in acesta sectiune corespund unei codificari de tip special: codificarea unei litere nu este prefixul codificarii nici unei alte litere. O astfel de codificare este de tip prefix. Codul Morse nu face parte din aceasta categorie. Codificarea cea mai compacta a unui sir de caractere poate fi intotdeauna obtinuta printr-un cod de tip prefix. Deci, concentrandu-ne atentia asupra acestei categorii de coduri, nu am pierdut nimic din generalitate.

6.6 Arbori partiali de cost minim

Fie G = <V, M> un graf neorientat conex, unde V este multimea varfurilor si M este multimea muchiilor. Fiecare muchie are un cost nenegativ (sau o lungime nenegativa). Problema este sa gasim o submultime A Í M, astfel incat toate varfurile din V sa ramina conectate atunci cand sunt folosite doar muchii din A, iar suma lungimilor muchiilor din A sa fie cat mai mica. Cautam deci o submultime A de cost total minim. Aceasta problema se mai numeste si problema conectarii oraselor cu cost minim, avand numeroase aplicatii.

Graful partial <V, A> este un arbore (Exercitiul 6.11) si este numit arborele partial de cost minim al grafului G (minimal spanning tree). Un graf poate avea mai multi arbori partiali de cost minim si acest lucru se poate verifica pe un exemplu.

Vom prezenta doi algoritmi greedy care determina arborele partial de cost minim al unui graf. In terminologia metodei greedy, vom spune ca o multime de muchii este o solutie, daca constituie un arbore partial al grafului G, si este fezabila, daca nu contine cicluri. O multime fezabila de muchii este promitatoare, daca poate fi completata pentru a forma solutia optima. O muchie atinge o multime data de varfuri, daca exact un capat al muchiei este in multime. Urmatoarea proprietate va fi folosita pentru a demonstra corectitudinea celor doi algoritmi.

Proprietatea 6.2 Fie G = <V, M> un graf neorientat conex in care fiecare muchie are un cost nenegativ. Fie W Ì V o submultime stricta a varfurilor lui G si fie A Í M o multime promitatoare de muchii, astfel incat nici o muchie din A nu atinge W. Fie m muchia de cost minim care atinge W. Atunci, A È {m} este promitatoare.

Demonstratie: Fie B un arbore partial de cost minim al lui G, astfel incat A Í B (adica, muchiile din A sunt continute in arborele B). Un astfel de B trebuie sa existe, deoarece A este promitatoare. Daca m Î B, nu mai ramane nimic de demonstrat. Presupunem ca m Ï B. Adaugandu-l pe m la B, obtinem exact un ciclu (Exercitiul3.2). In acest ciclu, deoarece m atinge W, trebuie sa mai existe cel putin o muchie m' care atinge si ea pe W (altfel, ciclul nu se inchide). Eliminandu-l pe m', ciclul dispare si obtinem un nou arbore partial B' al lui G. Costul lui m este mai mic sau egal cu costul lui m', deci costul total al lui B' este mai mic sau egal cu costul total al lui B. De aceea, B' este si el un arbore partial de cost minim al lui G, care include pe m. Observam ca A Í B' deoarece muchia m', care atinge W, nu poate fi in A. Deci, A È {m} este promitatoare. 

Multimea initiala a candidatilor este M. Cei doi algoritmi greedy aleg muchiile una cate una intr-o anumita ordine, aceasta ordine fiind specifica fiecarui algoritm.

6.6.1 Algoritmul lui Kruskal

Arborele partial de cost minim poate fi construit muchie, cu muchie, dupa urmatoarea metoda a lui Kruskal (1956): se alege intai muchia de cost minim, iar apoi se adauga repetat muchia de cost minim nealeasa anterior si care nu formeaza cu precedentele un ciclu. Alegem astfel #V–1 muchii. Este usor de dedus ca obtinem in final un arbore (revedeti Exercitiul 3.2). Este insa acesta chiar arborele partial de cost minim cautat?

Inainte de a raspunde la intrebare, sa consideram, de exemplu, graful din Figura 6.4a. Ordonam crescator (in functie de cost) muchiile grafului: {1, 2}, {2, 3}, {4, 5}, {6, 7}, {1, 4}, {2, 5}, {4, 7}, {3, 5}, {2, 4}, {3, 6}, {5, 7}, {5, 6} si apoi aplicam algoritmul. Structura componentelor conexe este ilustrata, pentru fiecare pas, in Tabelul 6.1.

Multimea A este initial vida si se completeaza pe parcurs cu muchii acceptate (care nu formeaza un ciclu cu muchiile deja existente in A). In final, multimea A va contine muchiile {1, 2}, {2, 3}, {4, 5}, {6, 7}, {1, 4}, {4, 7}. La fiecare pas, graful partial <V, A> formeaza o padure de componente conexe, obtinuta din padurea precedenta unind doua componente. Fiecare componenta conexa este la randul ei un arbore partial de cost minim pentru varfurile pe care le conecteaza. Initial, fiecare varf formeaza o componenta conexa. La sfarsit, vom avea o singura componenta conexa, care este arborele partial de cost minim cautat (Figura 6.4b).

Ceea ce am observat in acest caz particular este valabil si pentru cazul general, din Proprietatea 6.2 rezultand:

Proprietatea 6.3 In algoritmul lui Kruskal, la fiecare pas, graful partial <V, A> formeaza o padure de componente conexe, in care fiecare componenta conexa este la randul ei un arbore partial de cost minim pentru varfurile pe care le conecteaza. In final, se obtine arborele partial de cost minim al grafului G. 

Pentru a implementa algoritmul, trebuie sa putem manipula submultimile formate din varfurile componentelor conexe. Folosim pentru aceasta o structura de multimi disjuncte si procedurile de tip find si merge (Sectiunea 3.5). In acest caz, este preferabil sa reprezentam graful ca o lista de muchii cu costul asociat lor, astfel incat sa putem ordona aceasta lista in functie de cost. Iata algoritmul:

function Kruskal(G = <V, M>)
     {initializare}
     sorteaza M crescator in functie de cost
     n ¬ #V
     A ¬ Æ {va contine muchiile arborelui partial de cost minim}
     initializeaza n multimi disjuncte continand
          fiecare cate un element din V

     {bucla greedy}
     repeat
          {u, v} ¬ muchia de cost minim care
                            inca nu a fost considerata
          ucomp ¬ find(u)
          vcomp ¬ find(v)
          if ucomp ¹ vcomp     then   merge(ucomp, vcomp)
                                               A ¬ A È {{u, v}}
     until #A = n-1
     return A

Pentru un graf cu n varfuri si m muchii, presupunand ca se folosesc procedurile find3 si merge3, numarul de operatii pentru cazul cel mai nefavorabil este in:

·    O(m log m) pentru a sorta muchiile. Deoarece m £ n(n–1)/2, rezulta O(m log m) Í O(m log n). Mai mult, graful fiind conex, din n-1 £ m rezulta si O(m log n) Í O(m log m), deci O(m log m) = O(m log n).
·    O(n) pentru a initializa cele n multimi disjuncte.
·    Cele cel mult 2m operatii find3 si n–1 operatii merge3 necesita un timp in O((2m+n-1) lg* n), dupa cum am specificat in Capitolul 3. Deoarece O(lg* n) Í O(log n) si n-1 £ m, acest timp este si in O(m log n).
·    O(m) pentru restul operatiilor.

Deci, pentru cazul cel mai nefavorabil, algoritmul lui Kruskal necesita un timp in O(m log n).

O alta varianta este sa pastram muchiile intr-un min-heap. Obtinem astfel un nou algoritm, in care initializarea se face intr-un timp in O(m), iar fiecare din cele n–1 extrageri ale unei muchii minime se face intr-un timp in O(log m) = O(log n). Pentru cazul cel mai nefavorabil, ordinul timpului ramane acelasi cu cel al vechiului algoritm. Avantajul folosirii min-heap-ului apare atunci cand arborele partial de cost minim este gasit destul de repede si un numar considerabil de muchii raman netestate. In astfel de situatii, algoritmul vechi pierde timp, sortand in mod inutil si aceste muchii.

6.6.2 Algoritmul lui Prim

Cel de-al doilea algoritm greedy pentru determinarea arborelui partial de cost minim al unui graf se datoreaza lui Prim (1957). In acest algoritm, la fiecare pas, multimea A de muchii alese impreuna cu multimea U a varfurilor pe care le conecteaza formeaza un arbore partial de cost minim pentru subgraful <U, A> al lui G. Initial, multimea U a varfurilor acestui arbore contine un singur varf oarecare din V, care va fi radacina, iar multimea A a muchiilor este vida. La fiecare pas, se alege o muchie de cost minim, care se adauga la arborele precedent, dand nastere unui nou arbore partial de cost minim (deci, exact una dintre extremitatile acestei muchii este un varf in arborele precedent). Arborele partial de cost minim creste “natural”, cu cate o ramura, pina cand va atinge toate varfurile din V, adica pina cand U = V. Functionarea algoritmului, pentru exemplul din Figura 6.4a, este ilustrata in Tabelul 6.2. La sfarsit, A va contine aceleasi muchii ca si in cazul algoritmului lui Kruskal. Faptul ca algoritmul functioneaza intotdeauna corect este exprimat de urmatoarea proprietate, pe care o puteti demonstra folosind Proprietatea 6.2.

Proprietatea 6.4 In algoritmul lui Prim, la fiecare pas, <U, A> formeaza un arbore partial de cost minim pentru subgraful <U, A> al lui G. In final, se obtine arborele partial de cost minim al grafului G. 

 
Descrierea formala a algoritmului este data in continuare.

function Prim-formal(G = <V, M>)
     {initializare}
     A ¬ Æ   {va contine muchiile arborelui partial de cost minim}
     U ¬ {un varf oarecare din V}
     {bucla greedy}
     while U ¹ V do
          gaseste {u, v} de cost minim astfel ca u Î V \ U si v Î U
          A ¬ A È {{u, v}}
          U ¬ U È {u}
     return A

Pentru a obtine o implementare simpla, presupunem ca: varfurile din V sunt numerotate de la 1 la n, V = {1, 2, ..., n}; matricea simetrica C da costul fiecarei muchii, cu C[i, j] = +¥, daca muchia {i, j} nu exista. Folosim doua tablouri paralele. Pentru fiecare i Î V \ U, vecin[i] contine varful din U, care este conectat de i printr-o muchie de cost minim; mincost[i] da acest cost. Pentru i Î U, punem mincost[i] = –1. Multimea U, in mod arbitrar initializata cu {1}, nu este reprezentata explicit. Elementele vecin[1] si mincost[1] nu se folosesc.

function Prim(C[1 .. n, 1 .. n])
     {initializare; numai varful 1 este in U}
     A ¬ Æ
     for i ¬ 2 to n do   vecin[i]    ¬ 1
                                 mincost[i] ¬ C[i, 1]
     {bucla greedy}
     repeat n–1 times
          min ¬ +¥
          for j ¬ 2 to n do
              if 0 < mincost[ j] < min  then   min ¬ mincost[ j]
                                                              k ¬ j
          A ¬ A È {{k, vecin[k]}}
          mincost[k] ¬ –1  {adauga varful k la U}
          for j ¬ 2 to n do
              if C[k, j] < mincost[ j] then     mincost[ j] ¬ C[k, j]
                                                         vecin[ j] ¬ k
     return A

Bucla principala se executa de n–1 ori si, la fiecare iteratie, buclele for din interior necesita un timp in O(n). Algoritmul Prim necesita, deci, un timp in O(n²). Am vazut ca timpul pentru algoritmul lui Kruskal este in O(m log n), unde m = #M. Pentru un graf dens (adica, cu foarte multe muchii), se deduce ca m se apropie de n(n–1)/2. In acest caz, algoritmul Kruskal necesita un timp in O(n² log n) si algoritmul Prim este probabil mai bun. Pentru un graf rar (adica, cu un numar foarte mic de muchii), m se apropie de n si algoritmul Kruskal necesita un timp in O(n log n), fiind probabil mai eficient decat algoritmul Prim.

6.7 Implementarea algoritmului lui Kruskal

Functia care implementeaza algoritmul lui Kruskal in limbajul C++ este aproape identica cu procedura Kruskal din Sectiunea 6.6.1.

tablou<muchie> Kruskal( int n, const tablou<muchie>& M ) {
  heap<muchie> h( M );

  tablou<muchie> A( n - 1 ); int nA = 0;
  set            s( n );

  do {
    muchie m;
    if ( !h.delete_max( m ) )
      { cerr << "\n\nKruskal -- heap vid.\n\n"; return A = 0; }

    int ucomp = s.find3( m.u ),
        vcomp = s.find3( m.v );

    if ( ucomp != vcomp ) {
      s.merge3( ucomp, vcomp );
      A[ nA++ ] = m;
    }
  } while ( nA != n - 1 );

  return A;
}

Diferentele care apar sunt mai curand precizari suplimentare, absolut necesare in trecerea de la descrierea unui algoritm la implementarea lui. Astfel, graful este transmis ca parametru, prin precizarea numarului de varfuri si a muchiilor. Pentru muchii, reprezentate prin cele doua varfuri si costul asociat, am preferat in locul listei, structura simpla de tablou M, structura folosita si la returnarea arborelui de cost minim A.

Operatia principala efectuata asupra muchiilor este alegerea muchiei de cost minim care inca nu a fost considerata. Pentru implementarea acestei operatii, folosim un min-heap. La fiecare iteratie, se extrage din heap muchia de cost minim si se incearca inserarea ei in arborele A.

Ruland programul

main( ) {
  int n;
  cout << "\nVarfuri... ";
  cin >> n;

  tablou<muchie> M;
  cout << "\nMuchiile si costurile lor... ";
  cin >> M;

  cout << "\nArborele de cost minim Kruskal:\n";
  cout <<  Kruskal( n, M ) << '\n';
  return 1;
}

pentru graful din Figura 6.4 a, obtinem urmatoarele rezultate:

Arborele de cost minim Kruskal:
  [6]: { 1, 2; 1 } { 2, 3; 2 } { 4, 5; 3 } { 6, 7; 3 }
  { 1, 4; 4 } { 4, 7; 4 }

Clasa muchie, folosita in implementarea algoritmului lui Kruskal, trebuie sa permita:

·    Initializarea obiectelor, inclusiv cu valori implicite (initializare utila la construirea tablourilor de muchii).
·    Compararea obiectelor in functie de cost (operatie folosita de min-heap).
·    Operatii de citire si scriere (invocate indirect de operatorii respectivi din clasa tablou<T>).

Pornind de la aceste cerinte, se obtine urmatoarea implementare, continuta in fisierul muchie.h.

#ifndef __MUCHIE_H
#define __MUCHIE_H

class muchie {
public:
  muchie( int iu = 0, int iv = 0, float ic = 0. )
    { u = iu; v = iv; cost = ic; }

  int u, v;
  float cost;
};

inline operator >( const muchie& a, const muchie& b ) {
  return a.cost < b.cost;
}

inline istream& operator >>( istream& is, muchie& m ) {
  is >> m.u >> m.v >> m.cost; m.u--; m.v--;
  return is;
}

inline ostream& operator<< ( ostream& os, muchie& m ) {
  return os << "{ " << (m.u+1) << ", " << (m.v+1)
                               << "; " << m.cost << " }";
}

#endif

In ceea ce priveste clasa set, folosita si ea in implementarea algoritmului Kruskal, vom urma precizarile din Sectiunea 3.5 relative la manipularea multimilor disjuncte. Incapsularea, intr-o clasa, a structurii de multimi disjuncte si a procedurilor find3 si merge3 nu prezinta nici un fel de dificultati. Vom prezenta, totusi, implementarea clasei set, deoarece spatiul de memorie folosit este redus la jumatate.

La o analiza mai atenta a procedurii merge3, observam ca tabloul inaltimii arborilor este folosit doar pentru elementele care sunt si etichete de multimi (vezi Exercitiul 3.13). Aceste elemente, numite elemente canonice, sunt radacini ale arborilor respectivi. Altfel spus, un element canonic nu are tata si valoarea lui este folosita doar pentru a-l diferentia de elementele care nu sunt canonice. In Sectiunea3.5, elementele canonice sunt diferentiate prin faptul ca set[i] are valoarea i. Avand in vedere ca set[i] este indicele in tabloul set al tatalui elementului i, putem asocia elementelor canonice proprietatea set[i] < 0. Prin aceasta conventie, valoarea absoluta a elementelor canonice poate fi oarecare. Atunci, de ce sa nu fie chiar inaltimea arborelui?

In concluzie, pentru reprezentarea structurii de multimi disjuncte, este necesar un singur tablou, numit set, cu tot atatea elemente cate are si multimea. Valorile initiale ale elemetelor tabloului set sunt -1. Aceste initializari vor fi realizate prin constructor. Interfata publica a clasei set trebuie sa contina functiile merge3() si find3(), adaptate corepunzator. Tratarea situatiilor de exceptie care pot sa apara la invocarea acestor functii (indici de multimi in afara intervalului permis) se realizeaza prin activarea procedurii de verificare a indicilor in tabloul set.

Aceste considerente au condus la urmatoarele definitii ale functiilor membre din clasa set.

#include "set.h"

set::set( int n ): set( n ) {
  set.vOn( );
  for ( int i = 0; i < n; i++ )
    set[ i ] = -1;
}

void set::merge3( int a, int b ) {
  // sunt a si b etichete de multimi?
  if ( set[ a ] >= 0 ) a = find3( a );
  if ( set[ b ] >= 0 ) b = find3( b );

  // sunt multimile a si b diferite?
  if ( a == b ) return;

  // reuniunea propriu-zisa
  if ( set[ a ] == set[ b ] ) set[ set[ b ] = a ]--;
  else if ( set[ a ] < set[ b ] )  set[ b ] = a;
       else                        set[ a ] = b;

  return;
}

int set::find3( int x ) {
  int r = x;
  while ( set[ r ] >= 0 )
    r = set[ r ];

  int i = x;
  while ( i != r )
    { int j = set[ i ]; set[ i ] = r; i = j; }

  return r;
}

Fisierul header set.h este:

#ifndef __SET_H
#define __SET_H

#include "heap.h"

class set {
public:
  set( int );
  void merge3( int, int );
  int  find3 ( int );

private:
  tablou<int> set;
};

#endif

6.8 Cele mai scurte drumuri care pleaca din acelasi punct

Fie G = <V, M> un graf orientat, unde V este multimea varfurilor si M este multimea muchiilor. Fiecare muchie are o lungime nenegativa. Unul din varfuri este desemnat ca varf sursa. Problema este sa determinam lungimea celui mai scurt drum de la sursa catre fiecare varf din graf.

Vom folosi un algoritm greedy, datorat lui Dijkstra (1959). Notam cu C multimea varfurilor disponibile (candidatii) si cu S multimea varfurilor deja selectate. In fiecare moment, S contine acele varfuri a caror distanta minima de la sursa este deja cunoscuta, in timp ce multimea C contine toate celelalte varfuri. La inceput, S contine doar varful sursa, iar in final S contine toate varfurile grafului. La fiecare pas, adaugam in S acel varf din C a carui distanta de la sursa este cea mai mica.

Spunem ca un drum de la sursa catre un alt varf este special, daca toate varfurile intermediare de-a lungul drumului apartin lui S. Algoritmul lui Dijkstra lucreaza in felul urmator. La fiecare pas al algoritmului, un tablou D contine lungimea celui mai scurt drum special catre fiecare varf al grafului. Dupa ce adaugam un nou varf v la S, cel mai scurt drum special catre v va fi, de asemenea, cel mai scurt dintre toate drumurile catre v. Cand algoritmul se termina, toate varfurile din graf sunt in S, deci toate drumurile de la sursa catre celelalte varfuri sunt speciale si valorile din D reprezinta solutia problemei.

Presupunem, pentru simplificare, ca varfurile sunt numerotate, V = {1, 2, ..., n}, varful 1 fiind sursa, si ca matricea L da lungimea fiecarei muchii, cu L[i, j] = +¥, daca muchia (i, j) nu exista. Solutia se va construi in tabloul D[2 .. n]. Algoritmul este:

function Dijkstra(L[1 .. n, 1 .. n])
     {initializare}
     C ¬ {2, 3, ..., n}       {S = V \C exista doar implicit}
     for i ¬ 2 to n do D[i] ¬ L[1, i]
     {bucla greedy}
     repeat n–2 times
          v ¬ varful din C care minimizeaza D[v]
          C ¬ C \ {v}         {si, implicit, S ¬ S È {v}}
          for fiecare w Î C do
              D[w] ¬ min(D[w], D[v]+L[v, w])
     return D

Pentru graful din Figura 6.5, pasii algoritmului sunt prezentati in Tabelul 6.3.

Observam ca D nu se schimba daca mai efectuam o iteratie pentru a-l scoate si pe {2} din C. De aceea, bucla greedy se repeta de doar n-2 ori.

Se poate demonstra urmatoarea proprietate:

Proprietatea 6.5. In algoritmul lui Dijkstra, daca un varf i
i)     este in S, atunci D[i] da lungimea celui mai scurt drum de la sursa catre i;
ii)    nu este in S, atunci D[i] da lungimea celui mai scurt drum special de la sursa catre i. 

La terminarea algoritmului, toate varfurile grafului, cu exceptia unuia, sunt in S. Din proprietatea precedenta, rezulta ca algoritmul lui Dijkstra functioneaza corect.

Daca dorim sa aflam nu numai lungimea celor mai scurte drumuri, dar si pe unde trec ele, este suficient sa adaugam un tablou P[2 .. n], unde P[v] contine numarul nodului care il precede pe v in cel mai scurt drum. Pentru a gasi drumul complet, nu avem decat sa urmarim, in tabloul P, varfurile prin care trece acest drum, de la destinatie la sursa. Modificarile in algoritm sunt simple:

·    initializeaza P[i] cu 1, pentru 2 £ i £ n
·    continutul buclei for cea mai interioara se inlocuieste cu
if D[w] > D[v]+L[v, w]   then   D[w] ¬ D[v]+L[v, w]
                                               P[w] ¬ v
·    bucla repeat se executa de n-1 ori

Sa presupunem ca aplicam algoritmul Dijkstra asupra unui graf cu n varfuri si m muchii. Initializarea necesita un timp in O(n). Alegerea lui v din bucla repeat presupune parcurgerea tuturor varfurilor continute in C la iteratia respectiva, deci a n-1, n-2, ..., 2 varfuri, ceea ce necesita in total un timp in O(n²). Bucla for interioara efectueaza n-2, n-3, ..., 1 iteratii, totalul fiind tot in O(n²). Rezulta ca algoritmul Dijkstra necesita un timp in O(n²).

Incercam sa imbunatatim acest algoritm. Vom reprezenta graful nu sub forma matricii de adiacenta L, ci sub forma a n liste de adiacenta, continand pentru fiecare varf lungimea muchiilor care pleaca din el. Bucla for interioara devine astfel mai rapida, deoarece putem sa consideram doar varfurile w adiacente lui v. Aceasta nu poate duce la modificarea ordinului timpului total al algoritmului, daca nu reusim sa scadem si ordinul timpului necesar pentru alegerea lui v din bucla repeat. De aceea, vom tine varfurile v din C intr-un min-heap, in care fiecare element este de forma (v, D[v]), proprietatea de min-heap referindu-se la valoarea lui D[v]. Numim algoritmul astfel obtinut Dijkstra-modificat. Sa il analizam in cele ce urmeaza.

Initializarea min-heap-ului necesita un timp in O(n). Instructiunea “C ¬ C \ {v}” consta in extragerea radacinii min-heap-ului si necesita un timp in O(log n). Pentru cele n–2 extrageri este nevoie de un timp in O(n log n).

Pentru a testa daca “D[w] > D[v]+L[v, w]”, bucla for interioara consta acum in inspectarea fiecarui varf w din C adiacent lui v. Fiecare varf v din C este introdus in S exact o data si cu acest prilej sunt testate exact muchiile adiacente lui; rezulta ca numarul total de astfel de testari este de cel mult m. Daca testul este adevarat, trebuie sa il modificam pe D[w] si sa operam un percolate cu w in min-heap, ceea ce necesita din nou un timp in O(log n). Timpul total pentru operatiile percolate este deci in O(m log n).

In concluzie, algoritmul Dijkstra-modificat necesita un timp in O(max(n, m) log n). Daca graful este conex, atunci m ³ n si timpul este in O(m log n). Pentru un graf rar este preferabil sa folosim algoritmul Dijkstra-modificat, iar pentru un graf dens algoritmul Dijkstra este mai eficient.

Este usor de observat ca, intr-un graf G neorientat conex, muchiile celor mai scurte drumuri de la un varf i la celelalte varfuri formeaza un arbore partial al celor mai scurte drumuri pentru G. Desigur, acest arbore depinde de alegerea radacinii i si el difera, in general, de arborele partial de cost minim al lui G.

Problema gasirii celor mai scurte drumuri care pleaca din acelasi punct se poate pune si in cazul unui graf neorientat.

6.9 Implementarea algoritmului lui Dijkstra

Aceasta sectiune este dedicata implementarii algoritmului Dijkstra-modificat pentru determinarea celor mai scurte drumuri care pleaca din acelasi varf. Dupa cum am vazut, acest algoritm este de preferat in cazul grafurilor rare, timpul lui fiind in ordinul lui O(m log n), unde m este numarul de muchii, iar n numarul de varfuri ale unui graf conex.

In implementarea noastra, tipul de date “fundamental” este clasa vp (varf-pondere), definita cu ocazia implementarii arborilor de interclasare. Vom folosi aceasta clasa pentru:

·    Min-heap-ul C format din perechi (v, d), ponderea d fiind lungimea celui mai scurt drum special de la varful sursa la varful v.
·    Reprezentarea grafului G prin liste de adiacenta. Pentru fiecare varf v, perechea (w, l) este muchia de lungime l cu extremitatile in v si w.
·    Tabloul P, al rezultatelor. Elementul P[i], de valoare (v, d), reprezinta varful v care precede varful i in cel mai scurt drum de la varful sursa, d fiind lungimea acestui drum.

Graful G este implementat ca un tablou de liste de elemente de tip varf-pondere. Tipul graf, introdus prin

typedef tablou< lista<vp> > graf;

este un sinonim pentru aceasta structura.

Definitia de mai sus merita o clipa de atentie, deoarece exemplifica una din putinele exceptii lexicale din C++. In limbajul C++, ca si in limbajul C, notiunea de separator este inexistenta. Separarea atomilor lexicali ai limbajului (identificatori, operatori, cuvinte cheie, constante) prin caracterele “albe” spatiu sau tab este optionala. Totusi, in typedef-ul anterior, cele doua semne > trebuie separate, pentru a nu fi interpretate ca operatorul de decalare >>.

Manipularea grafului G, definit ca graf G, implica fixarea unui varf si apoi operarea asupra listei asociate varfului respectiv. Pentru o simpla parcurgere, nu avem decat sa definim iteratorul iterator<vp> g si sa-l initializam cu una din listele de adiacenta, de exemplu cu cea corespunzatoare varfului 2: g = G[ 2 ];.

Daca w este un obiect de tip vp, atunci, prin instructiunea

while( g( w ) ) {
  // ...
}

obiectul w va contine, rand pe rand, toate extremitatile si lungimile muchiilor care pleaca din varful 2.

Structura obiectului graf G asociat grafului din Figura 6.5, structura tiparita prin cout << G, este:

[5]:  { { 5; 10 } { 4; 100 } { 3; 30 } { 2; 50 } }
      { }
      { { 4; 50 } { 2; 5 } }
      { { 2; 20 } }
      { { 4; 10 } }

Executarea acestei instructiuni implica invocarea operatorilor de inserare << ai tuturor celor 3 clase implicate, adica vp, tablou<T> si lista<E>.

Citirea grafului G se realizeaza prin citirea muchiilor si inserarea lor in listele de adiacenta. In acest scop, vom folosi aceeasi clasa muchie, utilizata si in implementarea algoritmului lui Kruskal:

  int n, m = 0;  // #varfuri si #muchii
  muchie M;

  cout << "Numarul de varfuri... "; cin >> n;
  graf G( n );

  cout << "Muchiile... ";
  while( cin >> M ) {
    // aici se poate verifica corectitudinea muchiei M
    G[ M.u ].insert( vp( M.v, M.cost ) );
    m++;
  }

Algoritmul Dijkstra-modificat este implementat prin functia

tablou<vp> Dijkstra( const graf& G, int m, int s );

functie care returneaza tabloul tablou<vp> P(n). In lista de argumente a acestei functii, m este numarul de muchii, iar s este varful sursa. Dupa cum am mentionat, P[i].v (sau (int)P[i]) este varful care precede varful i pe cel mai scurt drum de la sursa catre i, iar P[i].p (sau (float)P[i]) este lungimea acestui drum. De exemplu, pentru acelasi graf din Figura 6.5, secventa:

for ( int s = 0; s < n; s++ ) {
    cout << "\nCele mai scurte drumuri de la varful "
         << (s + 1) << " sunt:\n";
    cout << Dijkstra( G, m, s ) << '\n';
  }

genereaza rezultatele:

Cele mai scurte drumuri de la varful 1 sunt:
[5]: { 1; 0 } { 3; 35 } { 1; 30 } { 5; 20 }
     { 1; 10 }

Cele mai scurte drumuri de la varful 2 sunt:

[5]: { 2; 3.37e+38 } { 1; 0 } { 2; 3.37e+38 }
     { 2; 3.37e+38 } { 2; 3.37e+38 }

Cele mai scurte drumuri de la varful 3 sunt:

[5]: { 3; 3.37e+38 } { 3; 5 } { 1; 0 } { 3; 50 }
     { 3; 3.37e+38 }

Cele mai scurte drumuri de la varful 4 sunt:

[5]: { 4; 3.37e+38 } { 4; 20 } { 4; 3.37e+38 }
     { 1; 0 } { 4; 3.37e+38 }

Cele mai scurte drumuri de la varful 5 sunt:

[5]: { 5; 3.37e+38 } { 4; 30 } { 5; 3.37e+38 }
     { 5; 10 } { 1; 0 }

unde 3.37e+38 este constanta MAXFLOAT din fisierul header <values.h>. MAXFLOAT este o aproximare rezonabila pentru +¥, fiind cel mai mare numar real admis de calculatorul pentru care se compileaza programul.

Datele locale functiei Dijkstra() sunt heap-ul heap<vp> C(n + m) si tabloul tablou<vp> P(n) al celor mai scurte drumuri (incluzand si distantele respective) de la fiecare din cele n varfuri la varful sursa. Initial, distantele din P[s] sunt +¥ (constanta MAXFLOAT din <values.h>), exceptand varful s si celelalte varfuri adiacente lui s, varfuri incluse si in heap-ul C. Initializarea variabilelor P si C este realizata prin secventa:

  vp w;

  // initializare
  for ( int i = 0; i < n; i++ )
    P[ i ] = vp( s, MAXFLOAT );
  for ( iterator<vp> g = G[ s ]; g( w ); )
    { C.insert( w ); P[ w ] = vp( s, w ); }
  P[ s ] = vp( 0, 0 );

Se observa aici invocarea explicita a constructorului clasei vp pentru initializarea elementelor tabloului P. Din pacate, initializarea nu este directa, ci prin intermediul unui obiect temporar de tip vp, obiect distrus dupa atribuire. Initializarea directa este posibila, daca vom completa clasa vp cu o functie de genul

vp& vp::set( int varf, float pondere )
  { v = varf; p = pondere; return *this; }

sau cu un operator

vp& vp::operator ( )( int varf, float pondere )
  { v = varf; p = pondere; return *this; }

Desi era mai natural sa folosim operatorul de atribuire =, nu l-am putut folosi deoarece este operator binar, iar aici avem nevoie de 3 operanzi: in membrul stang obiectul invocator si in membrul drept varful, impreuna cu ponderea. Folosind noul operator (),  secventa de initializare devine mai scurta si mai eficienta:

  vp w;

  // initializare
  for ( int i = 0; i < n; i++ )
    P[ i ]( s, MAXFLOAT );
  for ( iterator<vp> g = G[ s ]; g( w ); )
    { C.insert( w ); P[ w ]( s, w ); }
  P[ s ]( 0, 0 );

Bucla greedy a functiei Dijkstra()

  vp v;
  float dw;

  // bucla greedy
  for ( i = 1; i < n - 1; i++ ) {
    C.delete_max( v ); g = G[ v ];
    while ( g( w ) )
      if ( (float)P[ w ] > (dw = (float)P[ v ] + (float)w) )
        C.insert( vp( w, P[ w ]( v, dw ) ) );
  }

se obtine prin traducerea directa a descrierii algoritmului Dijkstra-modificat. Fiind dificil sa cautam in heap-ul C elemente (w, D[w]) dupa valoarea lui w, am inlocuit urmatoarele operatii:
i)     cautarea elementului (w, D[w]) pentru un w fixat
ii)    modificarea valorii D[w]
iii)  refacerea proprietatii de heap
cu o simpla inserare in heap a unui nou element (w, D[w]), D[w] fiind modificat corespunzator. Din pacate, aceasta simplificare poate mari heap-ul, deoarece exista posibilitatea ca pentru fiecare muchie sa fie inserat cate un nou element. Numarul de elemente din heap va fi insa totdeauna mai mic decat n + m. Timpul algoritmului ramane in O(m log n).

Crearea unui obiect temporar la inserarea in heap este justificata aici chiar prin algoritm. Conform precizarilor de mai sus, actualizarea distantelor se realizeaza indirect, prin inserarea unui nou obiect. Sa remarcam si inlocuirea tabloului redundant D cu membrul float din tabloul P.

In final, dupa executarea de n-2 ori a buclei greedy, functia Dijkstra() trebuie sa returneze tabloul P:

  return P;

Daca secventele prezentate pana acum nu va sunt suficiente pentru a scrie functia Dijkstra() si programul de test, iata forma lor completa:

#include <iostream.h>
#include <values.h>

#include "tablou.h"
#include "heap.h"
#include "muchie.h"
#include "lista.h"
#include "vp.h"

typedef tablou< lista<vp> > graf;

tablou<vp> Dijkstra( const graf& G, int m, int s ) {
  int n = G.size( );  // numarul de varfuri ale grafului G

  heap<vp> C( m );
  tablou<vp> P( n );

  vp v, w;   // muchii
  float dw;  // distanta

  // initializare
  for ( int i = 0; i < n; i++ )
    P[ i ]( s, MAXFLOAT );
  for ( iterator<vp> g = G[ s ]; g( w ); )
    C.insert( w ); P[ w ]( s, w );
  P[ s ]( 0, 0 );

  // bucla greedy
  for ( i = 1; i < n - 1; i++ ) {
    C.delete_max( v ); g = G[ v ];
    while ( g( w ) )
      if ( (float)P[ w ] > ( dw = (float)P[ v ] + (float)w ) )
        C.insert( vp( w, P[ w ]( v, dw ) ) );
  }
  return P;
}

main( ) {
  int n, m = 0;  // #varfuri si #muchii
  muchie M;

  cout << "Numarul de varfuri... "; cin >> n;
  graf G( n );

  cout << "Muchiile... ";
  while( cin >> M ) {
    // aici se poate verifica corectitudinea muchiei M
    G[ M.u ].insert( vp( M.v, M.cost ) );
    m++;
  }

  cout << "\nListele de adiacenta:\n"; cout << G << '\n';

  for ( int s = 0; s < n; s++ ) {
    cout << "\nCele mai scurte drumuri de la varful "
         << (s + 1) << " sunt:\n";
    cout << Dijkstra( G, m, s ) << '\n';
  }

  return 0;
}

6.10 Euristica greedy

Pentru anumite probleme, se poate accepta utilizarea unor algoritmi despre care nu se stie daca furnizeaza solutia optima, dar care furnizeaza rezultate “acceptabile”, sunt mai usor de implementat si mai eficienti decat algoritmii care dau solutia optima. Un astfel de algoritm se numeste euristic.

Una din ideile frecvent utilizate in elaborarea algoritmilor euristici consta in descompunerea procesului de cautare a solutiei optime in mai multe subprocese succesive, fiecare din aceste subprocese constand dintr-o optimizare. O astfel de strategie nu poate conduce intotdeauna la o solutie optima, deoarece alegerea unei solutii optime la o anumita etapa poate impiedica atingerea in final a unei solutii optime a intregii probleme; cu alte cuvinte, optimizarea locala nu implica, in general, optimizarea globala. Regasim, de fapt, principiul care sta la baza metodei greedy. Un algoritm greedy, despre care nu se poate demonstra ca furnizeaza solutia optima, este un algoritm euristic.

Vom da doua exemple de utilizare a algoritmilor greedy euristici.

6.10.1 Colorarea unui graf

Fie G = <V, M> un graf neorientat, ale carui varfuri trebuie colorate astfel incat oricare doua varfuri adiacente sa fie colorate diferit. Problema este de a obtine o colorare cu un numar minim de culori.

Folosim urmatorul algoritm greedy: alegem o culoare si un varf arbitrar de pornire, apoi consideram varfurile ramase, incercand sa le coloram, fara a schimba culoarea. Cand nici un varf nu mai poate fi colorat, schimbam culoarea si varful de start, repetand procedeul.

Daca in graful din Figura 6.6 pornim cu varful 1 si il coloram in rosu, mai putem colora tot in rosu varfurile 3 si 4. Apoi, schimbam culoarea si pornim cu varful 2, colorandu-l in albastru. Mai putem colora cu albastru si varful 5. Deci, ne-au fost suficiente doua culori. Daca coloram varfurile in ordinea 1, 5, 2, 3, 4, atunci se obtine o colorare cu trei culori.

Rezulta ca, prin metoda greedy, nu obtinem decat o solutie euristica, care nu este in mod necesar solutia optima a problemei. De ce suntem atunci interesati intr-o astfel de rezolvare? Toti algoritmii cunoscuti, care rezolva optim aceasta problema, sunt exponentiali, deci, practic, nu pot fi folositi pentru cazuri mari. Algoritmul greedy euristic propus furnizeaza doar o solutie “acceptabila”, dar este simplu si eficient.

Un caz particular al problemei colorarii unui graf corespunde celebrei probleme a colorarii hartilor: o harta oarecare trebuie colorata cu un numar minim de culori, astfel incat doua tari cu frontiera comuna sa fie colorate diferit. Daca fiecarui varf ii corespunde o tara, iar doua varfuri adiacente reprezinta tari cu frontiera comuna, atunci hartii ii corespunde un graf planar, adica un graf care poate fi desenat in plan fara ca doua muchii sa se intersecteze. Celebritatea problemei consta in faptul ca, in toate exemplele intalnite, colorarea s-a putut face cu cel mult 4 culori. Aceasta in timp ce, teoretic, se putea demonstra ca pentru o harta oarecare este nevoie de cel mult 5 culori. Recent [*] s-a demonstrat pe calculator faptul ca orice harta poate fi colorata cu cel mult 4 culori. Este prima demonstrare pe calculator a unei teoreme importante.

Problema colorarii unui graf poate fi interpretata si in contextul planificarii unor activitati. De exemplu, sa presupunem ca dorim sa executam simultan o multime de activitati, in cadrul unor sali de clasa. In acest caz, varfurile grafului reprezinta activitati, iar muchiile unesc activitatile incompatibile. Numarul minim de culori necesare pentru a colora graful corespunde numarului minim de sali necesare.

6.10.2 Problema comis-voiajorului

Se cunosc distantele dintre mai multe orase. Un comis-voiajor pleaca dintr-un oras si doreste sa se intoarca in acelasi oras, dupa ce a vizitat fiecare din celelalte orase exact o data. Problema este de a minimiza lungimea drumului parcurs. Si pentru aceasta problema, toti algoritmii care gasesc solutia optima sunt exponentiali.

Problema poate fi reprezentata printr-un graf neorientat, in care oricare doua varfuri diferite ale grafului sunt unite intre ele printr-o muchie, de lungime nenegativa. Cautam un ciclu de lungime minima, care sa se inchida in varful initial si care sa treaca prin toate varfurile grafului.

Conform strategiei greedy, vom construi ciclul pas cu pas, adaugand la fiecare iteratie cea mai scurta muchie disponibila cu urmatoarele proprietati:

·    nu formeaza un ciclu cu muchiile deja selectate (exceptand pentru ultima muchie aleasa, care completeaza ciclul)
·    nu exista inca doua muchii deja selectate, astfel incat cele trei muchii sa fie incidente in acelasi varf

De exemplu, pentru sase orase a caror matrice a distantelor este data in Tabelul 6.4, muchiile se aleg in ordinea: {1, 2}, {3, 5}, {4, 5}, {2, 3}, {4, 6}, {1, 6} si se obtine ciclul (1, 2, 3, 5, 4, 6, 1) de lungime 58. Algoritmul greedy nu a gasit ciclul optim, deoarece ciclul (1, 2, 3, 6, 4, 5, 1) are lungimea 56.

6.11 Exercitii

6.1       Presupunand ca exista monezi de:

i)     1, 5, 12 si 25 de unitati, gasiti un contraexemplu pentru care algoritmul greedy nu gaseste solutia optima;
ii)    10 si 25 de unitati, gasiti un contraexemplu pentru care algoritmul greedy nu gaseste nici o solutie cu toate ca exista solutie.

6.2       Presupunand ca exista monezi de:

k⁰, k¹, ..., k^n–1

unitati, pentru k Î N, k > 1 oarecare, aratati ca metoda greedy da mereu solutia optima. Considerati ca n este un numar finit si ca din fiecare tip de moneda exista o cantitate nelimitata.

6.3       Pe o banda magnetica sunt n programe, un program i de lungime l_i fiind apelat cu probabilitatea p_i, 1 £ i £ n, p₁+p₂+...+p_n = 1. Pentru a citi un program, trebuie sa citim banda de la inceput. In ce ordine sa memoram programele pentru a minimiza timpul mediu de citire a unui program oarecare?

Indicatie: Se pun in ordinea descrescatoare a rapoartelor p_i / l_i.

6.4       Analizati eficienta algoritmului greedy care planifica ordinea clientilor intr-o statie de servire, minimizand timpul mediu de asteptare.

6.5       Pentru un text format din n litere care apar cu frecventele f₁, f₂, ..., f_n, demonstrati ca arborele de codificare Huffman minimizeaza lungimea externa ponderata pentru toti arborii de codificare cu varfurile terminale avand valorile f₁, f₂, ..., f_n.

6.6       Cati biti ocupa textul “ABRACADABRA” dupa codificarea Huffman?

6.7       Ce se intampla cand facem o codificare Huffman a unui text binar? Ce se intampla cand facem o codificare Huffman a unui text format din litere care au aceeasi frecventa?

6.8       Elaborati algoritmul de compactare Huffman a unui sir de caractere.

6.9       Elaborati algoritmul de decompactare a unui sir de caractere codificat prin codul Huffman, presupunand ca se cunosc caracterele si codificarea lor. Folositi proprietatea ca acest cod este de tip prefix.

6.10     Pe langa codul Huffman, vom considera aici si un alt cod celebru, care nu se obtine insa printr-o metoda greedy, ci printr-un algoritm recursiv.

Un cod Gray este o secventa de 2ⁿ elemente astfel incat:

i)     fiecare element este un sir de n biti
ii)    oricare doua elemente sunt diferite
iii)  oricare doua elemente consecutive difera exact printr-un bit (primul element este considerat succesorul ultimului element)

Se observa ca un cod Gray nu este de tip prefix. Elaborati un algoritm recursiv pentru a construi codul Gray pentru orice n dat. Ganditi-va cum ati putea utiliza un astfel de cod.

Indicatie: Pentru n = 1 putem folosi secventa (0, 1). Presupunem ca avem un cod Gray pentru n–1, unde n > 1. Un cod Gray pentru n poate fi construit prin concatenarea a doua subsecvente. Prima se obtine prefixand cu 0 fiecare element al codului Gray pentru n–1. A doua se obtine citind in ordine inversa codul Gray pentru n–1 si prefixand cu 1 fiecare element rezultat.

6.11     Demonstrati ca graful partial definit ca arbore partial de cost minim este un arbore.

Indicatie: Aratati ca orice graf conex cu n varfuri are cel putin n–1 muchii si revedeti Exercitiul 3.2.

6.12     Daca in algoritmul lui Kruskal reprezentam graful nu printr-o lista de muchii, ci printr-o matrice de adiacenta, care contine costurile muchiilor, ce se poate spune despre timp?

6.13     Ce se intampla daca rulam algoritmul i) Kruskal, ii) Prim pe un graf neconex?

6.14     Ce se intampla in cazul algoritmului: i) Kruskal, ii) Prim daca permitem muchiilor sa aiba cost negativ?

6.15     Sa presupunem ca am gasit arborele partial de cost minim al unui graf G. Elaborati un algoritm de actualizare a arborelui partial de cost minim, dupa ce am adaugat in G un nou varf, impreuna cu muchiile incidente lui. Analizati algoritmul obtinut.

6.16     In graful din Figura 6.5, gasiti pe unde trec cele mai scurte drumuri de la varful 1 catre toate celelalte varfuri.

6.17     Scrieti algoritmul greedy pentru colorarea unui graf si analizati eficienta lui.

6.18     Ce se intampla cu algoritmul greedy din problema comis-voiajorului daca admitem ca pot exista doua orase fara legatura directa intre ele?

6.19     Scrieti algoritmul greedy pentru problema comis-voiajorului si analizati eficienta lui.

6.20     Intr-un graf orientat, un drum este hamiltonian daca trece exact o data prin fiecare varf al grafului, fara sa se intoarca in varful initial. Fie G un graf orientat, cu proprietatea ca intre oricare doua varfuri exista cel putin o muchie. Aratati ca in G exista un drum hamiltonian si elaborati algoritmul care gaseste acest drum.

6.21     Este cunoscut ca orice numar natural i poate fi descompus in mod unic intr-o suma de termeni ai sirului lui Fibonacci (teorema lui Zeckendorf). Daca prin k >> m notam k ³ m+2, atunci

                                             
unde
                                             k₁ >> k₂ >> ... >> k_r >> 0

In acesta reprezentare Fibonacci a numerelor, singura valoare posibila pentru este cel mai mare termen din sirul lui Fibonacci pentru care ; singura valoare posibila pentru  este cel mai mare termen pentru care  etc. Reprezentarea Fibonacci a unui numar nu contine niciodata doi termeni consecutivi ai sirului lui Fibonacci.

Pentru 0 £ i £ f_n–1, n ³ 3, numim codificarea Fibonacci de ordinul n al lui i secventa de biti b_n–1, b_n–2, ..., b₂, unde

este reprezentarea Fibonacci a lui i. De exemplu, pentru i = 6, codificarea de ordinul 6 este 1001, iar codificarea de ordinul 7 este 01001. Se observa ca in codificarea Fibonacci nu apar doi de 1 consecutiv.

Dati un algoritm pentru determinarea codificarii Fibonacci de ordinul n al lui i, unde n si i sunt oarecare.

6.22     Codul Fibonacci de ordinul n, n ³ 2, este secventa C_n a celor f_n codificari Fibonacci de ordinul n ale lui i, atunci cand i ia toate valorile 0 £ i £ f_n–1. De exemplu, daca notam cu l sirul nul, obtinem: C₂ = (l), C₃ = (0, 1), C₄ = (00, 01, 10), C₅ = (000, 001, 010, 100, 101) etc. Elaborati un algoritm recursiv care construieste codul Fibonacci pentru orice n dat. Ganditi-va cum ati putea  utiliza un astfel de cod.

Indicatie: Aratati ca putem construi codul Fibonacci de ordinul n, n ³ 4, prin concatenarea a doua subsecvente. Prima subsecventa se obtine prefixand cu 0 fiecare codificare din C_n-1. A doua subsecventa se obtine prefixand cu 10 fiecare codificare din C_n-2.

[*] K. Appel si W. Haken, in 1976.