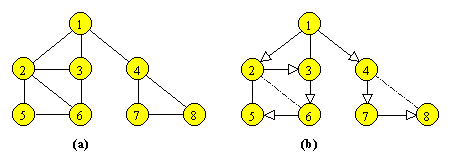
Figura 9.1 Un graf neorientat si unul din arborii sai partiali.
| Previous | Table of Contents | Next |
9. Explorari in grafuri
9.1 Parcurgerea arborilor
9.2 Operatii de parcurgere in clasa arbore<E>
9.3 Parcurgerea grafurilor in adancime
9.3.1 Puncte de articulare
9.3.2 Sortarea topologica
9.4 Parcurgerea grafurilor in latime
9.5 Salvarea si restaurarea arborilor binari
de cautare
9.6 Backtracking
9.7 Grafuri si jocuri
9.7.1 Jocul nim
9.7.2 Sahul si tehnica minimax
9.8 Grafuri AND/OR
9.9 Exercitii
Am vazut deja ca o mare varietate de probleme se formuleaza in termeni de grafuri. Pentru a le rezolva, de multe ori trebuie sa exploram un graf, adica sa consultam (vizitam) varfurile sau muchiile grafului respectiv. Uneori trebuie sa consultam toate varfurile sau muchiile, alteori trebuie sa consultam doar o parte din ele. Am presupus, pana acum, ca exista o anumita ordine a acestor consultari: cel mai apropiat varf, cea mai scurta muchie etc. In acest capitol, introducem cateva tehnici care pot fi folosite atunci cand nu este specificata o anumita ordine a consultarilor.
Vom folosi termenul de “graf” in doua ipostaze. Un graf va fi uneori, ca si pana acum, o structura de date implementata in memoria calculatorului. Acest mod explicit de reprezentare nu este insa indicat atunci cand graful contine foarte multe varfuri.
Sa presupunem, de exemplu, ca folosim varfurile unui graf pentru a reprezenta configuratii in jocul de sah, fiecare muchie corespunzand unei mutari legale intre doua configuratii. Acest graf are aproximativ 10120 varfuri. Presupunand ca un calculator ar fi capabil sa genereze 1011 varfuri pe secunda, generarea completa a grafului asociat jocului de sah s-ar face in mai mult de 1080 ani! Un graf atat de mare nu poate sa aiba decat o existenta implicita, abstracta.
Un graf implicit este un graf reprezentat printr-o descriere a varfurilor si muchiilor sale, el neexistand integral in memoria calculatorului. Portiuni relevante ale grafului pot fi construite pe masura ce explorarea progreseaza. De exemplu, putem avea in memorie doar o reprezentare a varfului curent si a muchiilor adiacente lui; pe masura ce inaintam in graf, vom actualiza aceasta reprezentare.
Tehnicile de explorare pentru cele doua concepte de graf (grafuri construite explicit si grafuri implicite) sunt, in esenta, identice. Indiferent de obiectivul urmarit, explorarea se realizeaza pe baza unor algoritmi de parcurgere, care asigura consultarea sistematica a varfurilor sau muchiilor grafului respectiv.
Pentru parcurgerea arborilor binari exista trei tehnici de baza. Daca pentru fiecare varf din arbore vizitam prima data varful respectiv, apoi varfurile din subarborele stang si, in final, subarborele drept, inseamna ca parcurgem arborele in preordine. Daca vizitam subarborele stang, varful respectiv si apoi subarborele drept, atunci parcurgem arborele in inordine, iar daca vizitam prima data subarborele stang, apoi cel drept, apoi varful respectiv, parcurgerea este in postordine. Toate aceste tehnici parcurg arborele de la stanga spre dreapta. Putem parcurge insa arborele si de la dreapta spre stanga, obtinand astfel inca trei moduri de parcurgere.
Proprietatea 9.1 Pentru fiecare din aceste sase tehnici
de parcurgere, timpul necesar pentru a explora un arbore binar cu n varfuri este in Q(n).
Demonstratie: Fie t(n) timpul necesar pentru parcurgerea unui arbore binar cu n varfuri. Putem presupune ca exista constanta reala pozitiva c, astfel incat t(n) £ c pentru 0 £ n £ 1. Timpul necesar pentru parcurgerea unui arbore cu n varfuri, n > 1, in care un varf este radacina, i varfuri sunt situate in subarborele stang si n-i-1 varfuri in subarborele drept, este
t(n) £ c + max {t(i)+t(n-i-1) | 0 £ i £ n-1}
Vom arata, prin inductie constructiva, ca t(n) £ dn+c, unde d este o alta constanta. Pentru n = 0, proprietatea este adevarata. Prin ipoteza inductiei specificate partial, presupunem ca t(i) £ di+c, pentru orice 0 £ i < n. Demonstram ca proprietatea este adevarata si pentru n. Avem
t(n) £ c+2c+d(n-1) = dn+c+2c-d
Luand d ³ 2c, obtinem t(n) £ dn+c. Deci, pentru d suficient de mare, t(n) £ dn+c, pentru orice n ³ 0, adica t Î O(n). Pe de alta parte, t Î W(n), deoarece fiecare din cele n varfuri trebuie vizitat. In consecinta, t Î Q(n).
Pentru fiecare din aceste tehnici de parcurgere, implementarea recursiva necesita,
in cazul cel mai nefavorabil, un spatiu de memorie in W(n)
(demonstrati acest lucru!). Cu putin efort[*], tehnicile mentionate pot fi implementate astfel
incat sa necesite un timp in Q(n) si un spatiu
de memorie in Q(1), chiar daca varfurile nu contin
adresa tatalui (caz in care problema devine triviala).
Conceptele de preordine si postordine se pot generaliza pentru arbori arbitrari (nebinari). Timpul de parcurgere este tot in ordinul numarului de varfuri.
Tipul abstract arbore este imposibil de conceput in lipsa unor metode sistematice de explorare. Iata cateva situatii in care le-am folosit, sau va trebui sa le folosim:
· Reorganizarea intr-un arbore
de cautare optim. Este vorba de procedura setvarf()
din clasa s8a (Sectiunea 8.7.1), procedura prin
care s-a initializat un tablou cu adresele tuturor varfurilor din arbore. Acum
este clar ca am folosit o parcurgere in inordine, prilej cu care am ajuns si
la o procedura de sortare similara quicksort-ului.
· Copierea, varf cu varf, a unui
arbore intr-un alt arbore. Procedura este necesara constructorului si operatorului
de atribuire.
· Implementarea destructorului
clasei, adica eliberarea spatiului ocupat de fiecare din varfurile arborelui.
· Afisarea unor “instantanee”
ale structurii arborilor pentru a verifica corectitudinea diverselor operatii.
Operatia de copiere este implementata prin functia _copy() din clasa varf<E>. Este vorba de o functie care copiaza recursiv arborele al carui varf radacina este dat ca argument, iar apoi returneaza adresa arborelui construit prin copiere.
template <class E>
varf<E>* _copy( varf<E>* x ) {
varf<E> *z = 0;
if ( x ) {
// varful nou alocat se initializeaza cu x
z = new varf<E>( x->key, x->p );
// se copiaza subarborii din stanga si din deapta; in
// fiecare se initializeaza legatura spre varful tata
if ( (z->st = _copy( x->st )) != 0 )
z->st->tata = z;
if ( (z->dr = _copy( x->dr )) != 0 )
z->dr->tata = z;
}
return z;
}
Invocarea acestei functii este realizata atat de catre constructorul de copiere al clasei arbore,
template <class E>
arbore<E>::arbore( const arbore<E>& a ) {
root = _copy( a.root ); n = a.n;
}
cat si de catre operatorul de atribuire:
template <class E>
arbore<E>& arbore<E>::operator =( const arbore<E>&
a ) {
delete root;
root = _copy( a.root ); n = a.n;
return *this;
}
Efectul instructiunii delete root ar trebui sa fie stergerea tuturor varfurilor din arborele cu radacina root. Pentru a ajunge la acest rezultat, avem nevoie de implementarea corespunzatoare a destructorului clasei varf<E>, destructor invocat, dupa cum se stie, inainte ca operatorul delete sa elibereze spatiul alocat. Forma acestui destructor este foarte simpla:
~varf( ) { delete st; delete dr; }
Efectul lui consta in stergerea varfurilor in postordine. Mai intai, se actioneaza asupra sub-arborelui stang, apoi asupra celui drept, iar in final, dupa executia corpului destructorului, operatorul delete elibereaza spatiul alocat varfului curent. Conditia de oprire a recursivitatii este asigurata de operatorul delete, el fiind inefectiv pentru adresele nule. In consecinta, si destructorul clasei arbore<E> consta intr-un simplu delete root:
~arbore( ) { delete root; }
Toate modalitatile de parcurgere mentionate in Sectiunea 9.1pot fi implementate imediat, prin functiile corespunzatoare. Noi ne-am rezumat la implementarea parcurgerii in inordine deoarece, pe parcursul testarii clasei arbore<E>, am avut nevoie de afisarea structurii arborelui. Functia
template <class E>
void _inord( varf<E> *x ) {
if ( !x ) return;
_inord( x->st );
cout << x
<< " ( key " << x->key
<< ", f " << x->p
<< ", st " << x->st
<< ", dr " << x->dr
<< ", tata " << x->tata
<< " )";
_inord( x->dr );
}
apelabila din clasa arbore<E> prin
template <class E>
void arbore<E>::inord( ) { _inord( root ); }
este exact ceea ce ne trebuie pentru a afisa intreaga structura interna a arborelui.
Fie G = <V, M> un graf orientat sau neorientat, ale carui varfuri dorim sa le consultam. Presupunem ca avem posibilitatea sa marcam varfurile deja vizitate in tabloul global marca. Initial, nici un varf nu este marcat.
Pentru a efectua o parcurgere in adancime, alegem un varf oarecare, v Î V, ca punct de plecare si il marcam. Daca exista un varf w adiacent lui v (adica, daca exista muchia (v, w) in graful orientat G, sau muchia {v, w} in graful neorientat G) care nu a fost vizitat, alegem varful w ca noul punct de plecare si apelam recursiv procedura de parcurgere in adancime. La intoarcerea din apelul recursiv, daca exista un alt varf adiacent lui v care nu a fost vizitat, apelam din nou procedura etc. Cand toate varfurile adiacente lui v au fost marcate, se incheie consultarea inceputa in v. Daca au ramas varfuri in V care nu au fost vizitate, alegem unul din aceste varfuri si apelam procedura de parurgere. Continuam astfel, pana cand toate varfurile din V au fost marcate. Iata algoritmul:
procedure parcurge(G)
for
fiecare v Î V do marca[v] ¬ nevizitat
for
fiecare v Î V do
if marca[v] = nevizitat
then ad(v)
procedure ad(v)
{virful v nu a fost vizitat}
marca[v] ¬ vizitat
for
fiecare virf w adiacent lui v do
if marca[w] = nevizitat
then ad(w)
Acest mod de parcurgere se numeste “in adancime”, deoarece incearca sa initieze cat mai multe apeluri recursive inainte de a se intoarce dintr-un apel.
Parcurgerea in adancime a fost formulata cu mult timp in urma ca o tehnica de explorare a unui labirint. O persoana care cauta ceva intr-un labirint si aplica aceasta tehnica are avantajul ca “urmatorul loc in care cauta” este mereu foarte aproape.
Pentru graful din Figura 9.1a, presupunand ca pornim din varful 1 si ca vizitam vecinii unui varf in ordine numerica, parcurgerea varfurilor in adancime se face in ordinea: 1, 2, 3, 6, 5, 4, 7, 8.
|
Figura 9.1 Un graf neorientat si unul din arborii sai partiali. |
Desigur, parcurgerea in adancime a unui graf nu este unica; ea depinde atat de alegerea varfului initial, cat si de ordinea de vizitare a varfurilor adiacente.
Cat timp este necesar pentru a parcurge un graf cu n varfuri si m muchii? Deoarece fiecare varf este vizitat exact o data, avem n apeluri ale procedurii ad. In procedura ad, cand vizitam un varf, testam marcajul fiecarui vecin al sau. Daca reprezentam graful prin liste de adiacenta, adica prin atasarea la fiecare varf a listei de varfuri adiacente lui, atunci numarul total al acestor testari este: m, daca graful este orientat, si 2m, daca graful este neorientat. Algoritmul necesita un timp in Q(n) pentru apelurile procedurii ad si un timp in Q(m) pentru inspectarea marcilor. Timpul de executie este deci in Q(max(m, n)) = Q(m+n).
Daca reprezentam graful printr-o matrice de adiacenta, se obtine un timp de executie in Q(n2).
Parcurgerea in adancime a unui graf G, neorientat si conex, asociaza lui G un arbore partial. Muchiile arborelui corespund muchiilor parcurse in G, iar varful ales ca punct de plecare devine radacina arborelui. Pentru graful din Figura 9.1a, un astfel de arbore este reprezentat in Figura 9.1b prin muchiile “continue”; muchiile din G care nu corespund unor muchii ale arborelui sunt “punctate”. Daca graful G nu este conex, atunci parcurgerea in adancime asociaza lui G o padure de arbori, cate unul pentru fiecare componenta conexa a lui G.
Daca dorim sa si marcam numeric varfurile in ordinea parcurgerii lor, adaugam in procedura ad, la inceput:
num ¬ num + 1
preord[v] ¬ num
unde num este o variabila globala initializata cu zero, iar preord[1 .. n] este un tablou care va contine in final ordinea de parcurgere a varfurilor. Pentru parcurgerea din exemplul precedent, acest tablou devine:
|
1 |
2 |
3 |
6 |
5 |
4 |
7 |
8 |
Cu alte cuvinte, se parcurg in preordine varfurile arborelui partial din Figura 9.1b.
Se poate observa ca parcurgerea in adancime a unui arbore, pornind din radacina, are ca efect parcurgerea in preordine a arborelui.
Parcurgerea in adancime se dovedeste utila in numeroase probleme din teoria grafurilor, cum ar fi: detectarea componentelor conexe (respectiv, tare conexe) ale unui graf, sau verificarea faptului ca un graf este aciclic. Ca exemplu, vom rezolva in aceasta sectiune problema gasirii punctelor de articulare ale unui graf conex.
Un varf v al unui graf neorientat conex este un punct de articulare, daca subgraful obtinut prin eliminarea lui v si a muchiilor care pleca din v nu mai este conex. De exemplu, varful 1 este un punct de articulare pentru graful din Figura 9.1. Un graf neorientat este biconex (sau nearticulat) daca este conex si nu are puncte de articulare. Grafurile biconexe au importante aplicatii practice: daca o retea de telecomunicatii poate fi reprezentata printr-un graf biconex, aceasta ne garanteaza ca reteaua continua sa functioneze chiar si dupa ce echipamentul dintr-un varf s-a defectat.
Este foarte util sa putem verifica eficient daca un graf are puncte de articulare. Urmatorul algoritm gaseste punctele de articulare ale unui graf conex G.
1. Efectueaza o parcurgere in adancime a lui G pornind dintr-un varf oarecare. Fie A arborele partial generat de aceasta parcurgere si preord tabloul care contine ordinea de parcurgere a varfurilor.
2. Parcurge arborele A in postordine. Pentru fiecare varf v vizitat, calculeaza minim[v] ca minimul dintre
· preord[v]
· preord[w] pentru
fiecare varf w pentru care exista o muchie {v, w}
in G care nu are o muchie corespunzatoare in A (in Figura 9.1b,
o muchie “punctata”)
· minim[x] pentru
fiecare fiu x al lui v in A
3. Punctele de articulare se determina acum astfel:
a. radacina lui A este un punct de articulare al lui G,
daca si numai daca are mai mult de un fiu;
b. un varf v diferit de radacina lui A este un punct
de articulare al lui G, daca si numai daca v are un fiu x,
astfel incat minim[x] ³ preord[v].
Pentru exemplul din Figura 9.1b, rezulta ca tabloul minim este
|
1 |
1 |
1 |
6 |
2 |
2 |
6 |
6 |
iar varfurile 1 si 4 sunt puncte de articulare.
Pentru a demonstra ca algoritmul este corect, enuntam pentru inceput o proprietate care rezulta din Exercitiul 9.8: orice muchie din G, care nu are o muchie corespunzatoare in A, conecteza in mod necesar un varf v cu un ascendent al sau in A. Tinand cont de aceasta proprietate, valoarea minim[v] se poate defini si astfel:
minim[v] = min{preord[w] | se poate
ajunge din v in w urmand oricate
muchii “continue”, iar apoi urmand
“in sus”
cel mult o muchie “punctata”}
Alternativa 3a din algoritm rezulta
imediat, deoarece este evident ca radacina lui A este un punct de articulare al lui G, daca si numai daca are mai mult de un fiu.
Sa presupunem acum ca v nu este radacina lui A. Daca x este un fiu al lui v si minim[x] < preord[v], rezulta ca exista o succesiune de muchii care il conecteza pe x cu celelalte varfuri ale grafului, chiar si dupa eliminarea lui v. Pe de alta parte, nu exista nici o succesiune de muchii care sa il conecteze pe x cu tatal lui v, daca minim[x] ³ preord[v]. Se deduce ca si alternativa 3b este corecta.
In aceasta sectiune, vom arata cum putem aplica parcurgerea in adancime a unui graf, intr-un procedeu de sortare esential diferit fata de sortarile intalnite pana acum.
Sa presupunem ca reprezentam diferitele stagii ale unui proiect complex printr-un graf orientat aciclic: varfurile sunt starile posibile ale proiectului, iar muchiile corespund activitatilor care se cer efectuate pentru a trece de la o stare la alta. Figura 9.2 da un exemplu al acestui mod de reprezentare. O sortare topologica a varfurilor unui graf orientat aciclic este o operatie de ordonare liniara a varfurilor, astfel incat, daca exista o muchie (i, j), atunci i apare inaintea lui j in aceasta ordonare.
|
|
Pentru graful din Figura 9.2, o sortare topologica este A, B, C, E, D, F, iar o alta este A, B, E, C, D, F. In schimb, secventa A, B, C, D, E, F nu este in ordine topologica.
Daca adaugam la sfirsitul procedurii ad linia
write v
atunci procedura de parcurgere in adancime va afisa varfurile in ordine topologica inversa. Pentru a intelege de ce se intimpla acest lucru, sa observam ca varful v este afisat dupa ce toate varfurile catre care exista o muchie din v au fost deja afisate.
Procedura de parcurgere in adancime, atunci cand se ajunge la un varf v oarecare, exploreaza prima data un varf w adiacent lui v, apoi un varf adiacent lui w etc. Pentru a efectua o parcurgere in latime a unui graf (orientat sau neorientat), aplicam urmatorul principiu: atunci cand ajungem intr-un varf oarecare v nevizitat, il marcam si vizitam apoi toate varfurile nevizitate adiacente lui v, apoi toate varfurile nevizitate adiacente varfurilor adiacente lui v etc. Spre deosebire de parcurgerea in adancime, parcurgerea in latime nu este in mod natural recursiva.
Pentru a putea compara aceste doua tehnici de parcurgere, vom da pentru inceput o versiune nerecursiva pentru procedura ad. Versiunea se bazeaza pe utilizarea unei stive. Presupunem ca avem functia ftop care returneaza ultimul varf inserat in stiva, fara sa il stearga. Folosim si functiile push si pop din Sectiunea 3.1.1.
procedure
iterad(v)
S ¬ stiva vida
marca[v] ¬ vizitat
push(v, S)
while
S nu este vida do
while exista un varf w adiacent lui ftop(S)
astfel incat marca[w] = nevizitat do
marca[w] ¬ vizitat
push(w, S)
pop(S)
Pentru parcurgerea in latime, vom utiliza o coada si functiile insert-queue, delete-queue din Sectiunea 3.1.2 . Iata acum algoritmul de parcurgere in latime:
procedure
lat(v)
C ¬ coada vida
marca[v] ¬ vizitat
insert-queue(v, C)
while
C nu este vida do
u ¬ delete-queue(C)
for fiecare virf w adiacent
lui u do
if marca[w] = nevizitat then marca[w] ¬ vizitat
insert-queue(w, C)
Procedurile iterad si lat trebuie apelate din procedura
procedure
parcurge(G)
for
fiecare v Î V do marca[v] ¬ nevizitat
for
fiecare v Î V do
if marca[v] = nevizitat
then {iterad sau lat} (v)
De exemplu, pentru graful din Figura 9.1, ordinea de parcurgere in latime a varfurilor este: 1, 2, 3, 4, 5, 6, 7, 8.
Ca si in cazul parcurgerii in adancime, parcurgerea in latime a unui graf G conex asociaza lui G un arbore partial. Daca G nu este conex, atunci obtinem o padure de arbori, cate unul pentru fiecare componenta conexa.
Analiza eficientei algoritmului de parcurgere in latime se face la fel ca pentru parcurgerea in adancime. Pentru a parcurge un graf cu n varfuri si m muchii timpul este in: i) Q(n+m), daca reprezentam graful prin liste de adiacenta; ii) Q(n2), daca reprezentam graful printr-o matrice de adiacenta.
Parcurgerea in latime este folosita de obicei atunci cand se exploreaza partial anumite grafuri infinite, sau cand se cauta cel mai scurt drum dintre doua varfuri.
Importanta operatiilor de salvare (backup) si restaurare (restore) este bine cunoscuta de catre toti utilizatorii de calculatoare. Intr-un fel sau altul, este bine ca informatiile sa fie arhivate periodic pe un suport extern, astfel ca, in caz de necesitate, sa le putem reconstitui cat mai usor. Pentru clasa arbore<E> am decis sa implementam operatiile de salvare si restaurare, in scopul de a facilita transferurile de arbori intre programe. Vom exemplifica cu aceasta ocazie, nu numai parcurgerea in latime, ci si lucrul cu fisiere binare, prin intermediul obiectelor de tip fstream din biblioteca standard de intrare/iesire a limbajului C++, obiecte declarate in fisierul header <fstream.h>.
Convenim sa memoram pe suportul extern atat cheia, cat si probabilitatea (frecventa) de acces a fiecarui varf. Scrierea se va face cheie dupa cheie (varf dupa varf), in ordinea obtinuta printr-un proces de vizitare a arborelui. Restaurarea arborelui este realizata prin inserarea fiecarei chei intr-un arbore initial vid. Citirea cheilor este secventiala, adica in ordinea in care au fost scrise in fisier.
Parcurgerile in adancime (in preordine) si in latime au proprietatea ca varful radacina al arborelui si al fiecarui subarbore este vizitat (si deci inserat) inaintea varfurilor fii. Avem astfel garantata reconstituirea corecta a arborelui de cautare, deoarece in momentul in care se insereaza o cheie oarecare, toate varfurile ascendente sunt deja inserate. In cele ce urmeaza, vom utiliza parcurgerea in latime.
Parcurgerea in latime a arborilor binari se face conform algoritmului din Sectiunea 9.4, cu specificarea ca, deoarece arborii sunt grafuri conexe si aciclice, nu mai este necesara marcarea varfurilor. In procedura de salvare,
template <class E>
int arbore<E>::save( char *file ) {
ofstream f( file, ios::binary ); // deschide fisierul
if ( !f ) return 0; // eroare la deschidere
coada<varf<E>*> c( n + 1 ); // ptr.
parcurgerea in latime
varf<E> *x; // varful curent
c.ins_q( root ); // primul element din coada
while ( c.del_q( x ) ) {
if ( !f.write( (char *) &(x->key), sizeof( x->key ) ) )
return 0; // eroare la scriere
if ( !f.write( (char *) &(x->p ), sizeof( x->p ) ) )
return 0; // eroare la scriere
if ( x->st ) c.ins_q( x->st );
if ( x->dr ) c.ins_q( x->dr );
}
f.close( );
return 1;
}
vizitarea unui varf consta in scrierea informatiilor asociate in fisierul de iesire. De aceasta data, nu vom mai folosi operatorii de iesire >> ai claselor E si float, ci vom copia, octet cu octet, imaginea binara a cheii si a probabilitatii asociate. Cheia este situata la adresa &(x->key) si are lungimea sizeof(x->key), sau sizeof(E). Probabilitatea este situata la adresa &(x->p) si are lungimea sizeof(x->p), sau sizeof(float). Operatia de scriere necesita un obiect de tip ofstream, output file stream, creat pe baza numelui fisierului char *file. Prin valoarea ios::binary din lista de argumente a constructorului clasei ofstream, fisierul va fi deschis in modul binar de lucru si nu in modul implicit text.
Functia de restaurare
template <class E>
int arbore<E>::rest( char *file ) {
ifstream f( file, ios::binary ); // deschide fisierul
if ( !f ) return 0; // eroare la deschidere
delete root;
root = 0; n = 0; // se va crea un nou arbore
E key; float p; // informatia din varful curent
while ( f.read( (char *) &key, sizeof( key ) ) &&
f.read( (char *) &p, sizeof( p ) ) )
ins( key, p );
f.close( );
return 1;
}
consta in deschiderea fisierului binar cu numele dat de parametrul char *file prin intermediul unui obiect de tip ifstream, input file stream, citirea celor doua componente ale fiecarui varf (cheia key si frecventa p) si inserarea varfului corespunzator in arbore. Neavand certitudinea ca initial arborele este vid, functia de restaurare sterge toate varfurile arborelui inainte de a incepe inserarea cheilor citite din fisier.
Testarea corectitudinii operatiilor din clasele ifstream si ofstream se realizeaza prin invocarea implicita a operatorului de conversie la int. Acest operator returneaza false, daca starea stream-lui corespunde unei erori, sau true, in caz contrar. Invocarea lui este implicita, deoarece functiile membre ifstream::read si ofstream::write returneaza obiectul invocator, iar sintaxa instructiunii while solicita o expresie de tip intreg. Acest operator de conversie la int este mostenit de la clasa ios, input-output stream, clasa din care sunt derivate toate celelalte clase utilizate pentru operatiile de intrare/iesire.
Backtracking (in traducere aproximativa, “cautare cu revenire”) este un principiu fundamental de elaborare a algoritmilor pentru probleme de optimizare, sau de gasire a unor solutii care indeplinesc anumite conditii. Algoritmii de tip backtracking se bazeaza pe o tehnica speciala de explorare a grafurilor orientate implicite. Aceste grafuri sunt de obicei arbori, sau, cel putin, nu contin cicluri.
Pentru exemplificare, vom considera o problema clasica: cea a plasarii a opt regine pe tabla de sah, astfel incat nici una sa nu intre in zona controlata de o alta. O metoda simplista de rezolvare este de a incerca sistematic toate combinatiile posibile de plasare a celor opt regine, verificand de fiecare data daca nu s-a obtinut o solutie. Deoarece in total exista
![]()
combinatii posibile, este evident ca acest mod de abordare nu este practic. O prima imbunatatire ar fi sa nu plasam niciodata mai mult de o regina pe o linie. Aceasta restrictie reduce reprezentarea pe calculator a unei configuratii pe tabla de sah la un simplu vector, posibil[1 .. 8]: regina de pe linia i, 1 £ i £ 8, se afla pe coloana posibil[i], adica in pozitia (i, posibil[i]). De exemplu, vectorul (3, 1, 6, 2, 8, 6, 4, 7) nu reprezinta o solutie, deoarece reginele de pe liniile trei si sase sunt pe aceeasi coloana si, de asemenea, exista doua perechi de regine situate pe aceeasi diagonala. Folosind acesta reprezentare, putem scrie in mod direct algoritmul care gaseste o solutie a problemei:
procedure regine1
for
i1 ¬ 1 to 8 do
for i2 ¬ 1 to 8 do
![]()
for i8 ¬ 1 to 8 do
posibil ¬ (i1, i2, …, i8)
if solutie(posibil) then write posibil
stop
write “nu exista solutie”
De aceasta data, numarul combinatiilor este redus la 88 = 16.777.216, algoritmul oprindu-se de fapt dupa ce inspecteaza 1.299.852 combinatii si gaseste prima solutie.
Vom proceda acum la o noua imbunatatire. Daca introducem si restrictia ca doua regine sa nu se afle pe aceeasi coloana, o configuratie pe tabla de sah se poate reprezenta ca o permutare a primilor opt intregi. Algoritmul devine
procedure regine2
posibil
¬ permutarea initiala
while
posibil ¹ permutarea finala and not
solutie(posibil) do
posibil ¬ urmatoarea permutare
if
solutie(posibil) then write
posibil
else write
“nu exista solutie”
Sunt mai multe posibilitati de a genera sistematic toate permutarile primilor n intregi. De exemplu, putem pune fiecare din cele n elemente, pe rand, in prima pozitie, generand de fiecare data recursiv toate permutarile celor n-1 elemente ramase:
procedure perm(i)
if
i = n then utilizeaza(T) {T
este o noua permutare}
else for j
¬ i to
n do interschimba T[i]
si T[ j]
perm(i+1)
interschimba
T[i]
si T[ j]
In algoritmul de generare a permutarilor, T[1 .. n] este un tablou global initializat cu [1, 2, …, n], iar primul apel al procedurii este perm(1). Daca utilizeaza(T) necesita un timp constant, atunci perm(1) necesita un timp in Q(n!).
Aceasta abordare reduce numarul de configuratii posibile la 8! = 40.320. Daca se foloseste algoritmul perm, atunci pana la prima solutie sunt generate 2830 permutari. Mecanismul de generare a permutarilor este mai complicat decat cel de generare a vectorilor de opt intregi intre 1 si 8. In schimb, verificarea faptului daca o configuratie este solutie se face mai usor: trebuie doar verificat daca nu exista doua regine pe aceeasi diagonala.
Chiar si cu aceste imbunatatiri, nu am reusit inca sa eliminam o deficienta comuna a algoritmilor de mai sus: verificarea unei configuratii prin “if solutie(posibil)” se face doar dupa ce toate reginele au fost deja plasate pe tabla. Este clar ca se pierde astfel foarte mult timp.
Vom reusi sa eliminam aceasta deficienta aplicand principiul backtracking. Pentru inceput, reformulam problema celor opt regine ca o problema de cautare intr-un arbore. Spunem ca vectorul P[1 .. k] de intregi intre 1 si 8 este k-promitator, pentru 0 £ k £ 8, daca zonele controlate de cele k regine plasate in pozitiile (1, P[1]), (2, P[2]), …, (k, P[k]) sunt disjuncte. Matematic, un vector P este k-promitator daca:
P[i] - P[ j] Ï {i - j, 0, j - i}, pentru orice 0 £ i, j £ k, i ¹ j
Pentru k £ 1, orice vector P este k-promitator. Solutiile problemei celor opt regine corespund vectorilor 8-promitatori.
Fie V multimea vectorilor k-promitatori, 0 £ k £ 8. Definim graful orientat G = <V, M> astfel: (P, Q) Î M, daca si numai daca exista un intreg k, 0 £ k £ 8, astfel incat P este k-promitator, Q este (k+1)-promitator si P[i] = Q[i] pentru fiecare 0 £ i £ k. Acest graf este un arbore cu radacina in vectorul vid (k = 0). Varfurile terminale sunt fie solutii (k = 8), fie varfuri “moarte” (k < 8), in care este imposibil de plasat o regina pe urmatoarea linie fara ca ea sa nu intre in zona controlata de reginele deja plasate. Solutiile problemei celor opt regine se pot obtine prin explorarea acestui arbore. Pentru aceasta, nu este necesar sa generam in mod explicit arborele: varfurile vor fi generate si abandonate pe parcursul explorarii. Vom parcurge arborele G in adancime, ceea ce este echivalent aici cu o parcurgere in preordine, “coborand” in arbore numai daca exista sanse de a ajunge la o solutie.
Acest mod de abordare are doua avantaje fata de algoritmul regine2. In primul rand, numarul de varfuri in arbore este mai mic decat 8!. Deoarece este dificil sa calculam teoretic acest numar, putem numara efectiv varfurile cu ajutorul calculatorului: #V = 2057. De fapt, este suficient sa exploram 114 varfuri pentru a ajunge la prima solutie. In al doilea rand, pentru a decide daca un vector este (k+1)-promitator, cunoscand ca este extensia unui vector k-promitator, trebuie doar sa verificam ca ultima regina adaugata sa nu fie pusa intr-o pozitie controlata de reginele deja plasate. Ca sa apreciem cat am castigat prin acest mod de verificare, sa observam ca in algoritmul regine2, pentru a decide daca o anumita permutare este o solutie, trebuia sa verificam fiecare din cele 28 de perechi de regine de pe tabla.
Am ajuns, in fine, la un algoritm performant, care afiseaza toate solutiile problemei celor opt regine. Din programul principal, apelam regine(0), presupunand ca posibil[1 .. 8] este un tablou global.
procedure regine(k)
{posibil[1 .. k] este k-promitator}
if
k = 8 then write posibil {este
o solutie}
else {exploreaza extensiile (k+1)-promitatoare
ale
lui posibil}
for j
¬ 1 to 8 do
if plasare(k, j) then posibil[k+1] ¬ j
regine(k+1)
function plasare(k, j)
{returneaza true, daca si numai daca se
poate plasa o regina in pozitia
(k+1, j)}
for
i ¬ 1 to k do
if j-posibil[i] Î {k+1-i, 0, i-k-1} then return false
return
true
Problema se poate generaliza, astfel incat sa plasam n regine pe o tabla de n linii si n coloane. Cu ajutorul unor contraexemple, puteti arata ca problema celor n regine nu are in mod necesar o solutie. Mai exact, pentru n £ 3 nu exista solutie, iar pentru n ³ 4 exista cel putin o solutie.
Pentru valori mai mari ale lui n, avantajul metodei backtracking este, dupa cum ne si asteptam, mai evident. Astfel, in problema celor douasprezece regine, algoritmul regine2 considera 479.001.600 permutari posibile si gaseste prima solutie la a 4.546.044 configuratie examinata. Arborele explorat prin algoritmul regine contine doar 856.189 varfuri, prima solutie obtinandu-se deja la vizitarea celui de-al 262-lea varf.
Algoritmii backtracking pot fi folositi si atunci cand solutiile nu au in mod necesar aceeasi lungime. Presupunand ca nici o solutie nu poate fi prefixul unei alte solutii, iata schema generala a unui algoritm backtracking:
procedure backtrack(v[1 .. k])
{v
este un vector k-promitator}
if
v este o solutie
then write v
else for fiecare vector w care
este (k+1)-promitator,
astfel incat w[1 .. k] = v[1 .. k]
do backtrack(w[1 .. k+1])
Exista foarte multe aplicatii ale algoritmilor backtracking. Puteti incerca astfel rezolvarea unor probleme intilnite in capitolele anterioare: problema colorarii unui graf, problema 0/1 a rucsacului, problema monezilor (cazul general). Tot prin backtracking puteti rezolva si o varianta a problemei comis-voiajorului, in care admitem ca exista orase fara legatura directa intre ele si nu se cere ca ciclul sa fie optim.
Parcurgerea in adancime, folosita in algoritmul regine, devine si mai avantajoasa atunci cand ne multumim cu o singura solutie a problemei. Sunt insa si probleme pentru care acest mod de explorare nu este avantajos.
Anumite probleme pot fi formulate sub forma explorarii unui graf implicit care este infinit. In aceste cazuri, putem ajunge in situatia de a explora fara sfarsit o anumita ramura infinita. De exemplu, in cazul cubului lui Rubik, explorarea manipularilor necesare pentru a trece dintr-o configuratie intr-alta poate cicla la infinit. Pentru a evita asemenea situatii, putem utiliza explorarea in latime a grafului. In cazul cubului lui Rubik, mai avem astfel un avantaj: obtinem in primul rand solutiile care necesita cel mai mic numar de manipulari. Aceasta idee este ilustrata de Exercitiul 9.15.
Am vazut ca algoritmii backtracking pot folosi atat explorarea in adancime cat si in latime. Ceea ce este specific tehnicii de explorare backtracking este testul de fezabilitate, conform caruia, explorarea anumitor varfuri poate fi abandonata.
Cele mai multe jocuri strategice pot fi reprezentate sub forma grafurilor orientate in care varfurile sunt pozitii in joc, iar muchiile sunt mutari legale intre doua pozitii. Daca numarul pozitiilor nu este limitat a priori, atunci graful este infinit. Vom considera in cele ce urmeaza doar jocuri cu doi parteneri, fiecare avand pe rand dreptul la o mutare. Presupunem, de asemenea, ca jocurile sunt simetrice (regulile sunt aceleasi pentru cei doi parteneri) si deterministe (nu exista un factor aleator).
Pentru a determina o strategie de castig intr-un astfel de joc, vom atasa fiecarui varf al grafului o eticheta care poate fi de castig, pierdere, sau remiza. Eticheta corespunde situatiei unui jucator care se afla in pozitia respectiva si trebuie sa mute. Presupunem ca nici unul din jucatori nu greseste, fiecare alegand mereu mutarea care este pentru el optima. In particular, din anumite pozitii ale jocului nu se poate efectua nici o mutare, astfel de pozitii terminale neavand pozitii succesoare in graf. Etichetele vor fi atasate in mod sistematic astfel:
· Etichetele atasate unei pozitii
terminale depind de jocul in cauza. De obicei, jucatorul care se afla intr-o
pozitie terminala a pierdut.
· O pozitie neterminala este o
pozitie de castig, daca cel putin una din pozitiile ei succesoare in graf este
o pozitie de pierdere.
· O pozitie neterminala este o
pozitie de pierdere, daca toate pozitiile ei succesoare in graf sunt pozitii
de castig.
· Orice pozitie care a ramas neetichetata
este o pozitie de remiza.
Daca jocul este reprezentat printr-un graf finit aciclic, aceasta metoda eticheteaza varfurile in ordine topologica inversa.
Vom ilustra aceste idei printr-o varianta a jocului nim. Initial, pe masa se afla cel putin doua bete de chibrit. Primul jucator ridica cel putin un bat, lasand pe masa cel putin un bat. In continuare, pe rand, fiecare jucator ridica cel putin un bat si cel mult de doua ori numarul de bete ridicate de catre partenerul de joc la mutarea anterioara. Castiga jucatorul care ridica ultimul bat. Nu exista remize.
O pozitie in acest joc este specificata atat de numarul de bete de pe tabla, cat si de numarul maxim de bete care pot fi ridicate la urmatoarea mutare. Varfurile grafului asociat jocului sunt perechi <i, j>, 1 £ j £ i, indicand ca pot fi ridicate cel mult j bete din cele i bete de pe masa. Din varful <i, j> pleaca j muchii catre varfurile <i-k, min(2k, i-k)>, 1 £ k £ j. Varful corespunzator pozitiei initiale intr-un joc cu n bete, n ³ 2, este <n, n-1>. Toate varfurile pentru care a doua componenta este zero corespund unor pozitii terminale, dar numai varful <0, 0> este interesant: varfurile <i, 0>, pentru i > 0, sunt inaccesibile. In mod similar, varfurile <i, j>, cu j impar si j < i-1, sunt inaccesibile. Varful <0, 0> corespunde unei pozitii de pierdere.
|
|
Figura 9.3 reprezinta graful corespunzator jocului cu cinci bete initiale: varfurile albe corespund pozitiilor de castig, varfurile gri corespund pozitiilor de pierdere, muchiile “continue” corespund mutarilor prin care se castiga, iar muchiile “punctate” corespund mutarilor prin care se pierde. Dintr-o pozitie de pierdere nu pleaca nici o muchie “continua”, aceasta corespunzand faptului ca din astfel de pozitii nu exista nici o mutare prin care se poate castiga.
Se observa ca jucatorul care are prima mutare intr-un joc cu doua, trei, sau cinci bete nu are nici o strategie de castig, dar are o astfel de strategie intr-un joc cu patru bete.
Urmatorul algoritm recursiv determina daca o pozitie este de castig.
function rec(i, j)
{returneaza true daca si numai daca varful
<i, j> reprezinta
o pozitie de castig;
presupunem ca 0 £ j £ i}
for
k ¬ 1 to j
do
if not rec(i-k, min(2k, i-k))
then return true
return
false
Algoritmul are acelasi defect ca si algoritmul fib1 (Capitolul 1): calculeaza in mod repetat anumite valori. De exemplu, rec(5, 4) returneaza false dupa ce a apelat succesiv
rec(4, 2), rec(3, 3), rec(2, 2), rec(1, 1)
Dar rec(3, 3) apeleaza, de asemenea, rec(2, 2) si rec(1, 1).
Putem evita acest lucru, construind prin programarea dinamica o matrice booleana globala, astfel incat G[i, j] = true, daca si numai daca <i, j> este o pozitie de castig. Fie n numarul maxim de bete folosite. Ca de obicei in programarea dinamica, calculam matricea G de jos in sus:
procedure din(n)
{calculeaza de jos in sus matricea G[1..n,
1..n]}
G[0, 0] ¬ false
for
i ¬ 1 to n do
for j ¬ 1 to i do
k ¬ 1
while k < j and G[i-k, min(2k, i-k)]
do k ¬ k+1
G[i, j] ¬ not
G[i-k, min(2k, i-k)]
Prin tehnica programarii dinamice, fiecare valoare a lui G este calculata o singura data. Pe de alta parte insa, in acest context multe din valorile lui G sunt calculate in mod inutil. Astfel, este inutil sa-l calculam pe G[i, j] atunci cand j este impar si j < i-1. Iata si un alt exemplu de calcul inutil: stim ca <15, 14> este o pozitie de castig, imediat ce am aflat ca al doilea succesor al sau, <13, 4>, este o pozitie de pierdere; valoarea lui G(12, 6) nu mai este utila in acest caz. Nu exista insa nici un rationament “de jos in sus” pentru a nu-l calcula pe G[12, 6]. Pentru a-l calcula pe G[15, 14], algoritmul din calculeaza 121 de valori G[i, j], insa utilizeaza efectiv doar 27 de valori.
Algoritmul recursiv rec este ineficient, deoarece calculeaza anumite valori in mod repetat. Pe de alta parte, datorita rationamentului “de sus in jos”, nu calculeaza niciodata valori pe care sa nu le si utilizeze.
Rezulta ca avem nevoie de o metoda care sa imbine avantajele formularii recursive cu cele ale programarii dinamice. Cel mai simplu este sa adaugam algoritmului recursiv o functie de memorie care sa memoreze daca un varf a fost deja vizitat sau nu. Pentru aceasta, definim matricea booleana globala init[0 .. n, 0 .. n], initializata cu false.
function nim(i, j)
if
init[i, j] then return G[i, j]
init[i, j] ¬ true
for
k ¬ 1 to j
do
if not nim(i-k, min(2k,
i-k)) then G[i, j] ¬ true
return true
G[i, j] ¬ false
return
false
Deoarece matricea init trebuie initializata, aparent nu am castigat nimic fata de algoritmul care foloseste programarea dinamica. Avantajul obtinut este insa mare, deoarece operatia de initializare se poate face foarte eficient, dupa cum vom vedea in Sectiunea 10.2.
Cand trebuie sa solutionam mai multe cazuri similare ale aceleiasi probleme, merita uneori sa calculam cateva rezultate auxiliare care sa poata fi apoi folosite pentru accelerarea solutionarii fiecarui caz. Aceasta tehnica se numeste preconditionare si este exemplificata in Exercitiul 9.7.
Jocul nim este suficient de simplu pentru a permite si o rezolvare mai eficienta decat prin algoritmul nim, fara a folosi graful asociat. Algoritmul de mai jos determina strategia de castig folosind preconditionarea. Intr-o pozitie initiala cu n bete, se apeleaza la inceput precond(n). Se poate arata ca un apel precond(n) necesita un timp in Q(n). Dupa aceea, orice apel mutare(i, j), 1 £ j £ i, returneaza intr-un timp in Q(1) cate bete sa fie ridicate din pozitia <i, j>, pentru o mutare de castig. Daca pozitia <i, j> este de pierdere, in mod conventional se indica ridicarea unui bat, ceea ce intirzie pe cat posibil pierderea inevitabila a jocului. Tabloul T [0 .. n] este global.
procedure precond(n)
T[0] ¬ ¥
for
i ¬ 1 to n do
k ¬ 1
while T[i-k] £ 2k
do k ¬ k+1
T[i] ¬ k
function mutare(i, j)
if
j < T[i]
then return 1 {prelungeste agonia!}
return
T[i]
Nu vom demonstra aici corectitudinea acestui algoritm.
Sahul este, desigur, un joc mult mai complex decat jocul nim. La prima vedere, graful asociat sahului contine cicluri. Exista insa reglementari ale Federatiei Internationale de Sah care previn intrarea intr-un ciclu. De exemplu, se declara remiza o partida dupa 50 de mutari in care nu are loc nici o actiune ireversibila (mutarea unui pion, sau eliminarea unei piese). Datorita acestor reguli, putem considera ca graful asociat sahului nu are cicluri.
Vom eticheta fiecare varf ca pozitie de castig pentru Alb, pozitie de castig pentru Negru, sau remiza. Odata construit, acest graf ne permite sa jucam perfect sah, adica sa castigam mereu, cand este posibil, si sa pierdem doar cand este inevitabil. Din nefericire (din fericire pentru jucatorii de sah), acest graf contine atatea varfuri, incat nu poate fi explorat complet nici cu cel mai puternic calculator existent.
Deoarece o cautare completa in graful asociat jocului de sah este imposibila, nu putem folosi tehnica programarii dinamice. Se impune atunci, in mod natural, aplicarea unei tehnici recursive, care sa modeleze rationamentul “de sus in jos”. Aceasta tehnica (numita minimax) este de tip euristic, si nu ne ofera certitudinea castigarii unei partide. Ideea de baza este urmatoarea: fiind intr-o pozitie oarecare, se alege una din cele mai bune mutari posibile, explorand doar o parte a grafului. Este de fapt o modelare a rationamentului unui jucator uman care gandeste doar cu un mic numar de mutari in avans.
Primul pas este sa definim o functie de evaluare statica eval, care atribuie o anumita valoare fiecarei pozitii posibile. In mod ideal, eval(u) va creste atunci cand pozitia u devine mai favorabila Albului. Aceasta functie trebuie sa tina cont de mai multi factori: numarul si calitatea pieselor existente de ambele parti, controlul centrului tablei, libertatea de miscare etc. Trebuie sa facem un compromis intre acuratetea acestei functii si timpul necesar calcularii ei. Cand se aplica unei pozitii terminale, functia de evaluare trebuie sa returneze +¥ daca a castigat Albul, -¥ daca a castigat Negrul si 0 daca a fost remiza.
Daca functia de evaluare statica ar fi perfecta, ar fi foarte usor sa determinam care este cea mai buna mutare dintr-o anumita pozitie. Sa presupunem ca este randul Albului sa mute din pozitia u. Cea mai buna mutare este cea care il duce in pozitia v, pentru care
eval(v) = max{eval(w) | w este succesor al lui u}
Aceasta pozitie se determina astfel:
val ¬ -¥
for fiecare w succesor al lui u do
if
eval(w) ³ val then val ¬ eval(w)
v ¬ w
Complexitatea jocului de sah este insa atat de mare incat este imposibil sa gasim o astfel de functie de evaluare perfecta.
Presupunand ca functia de evaluare nu este perfecta, o strategie buna pentru Alb este sa prevada ca Negrul va replica cu o mutare care minimizeaza functia eval. Albul gandeste astfel cu o mutare in avans, iar functia de evaluare este calculata in mod dinamic.
val ¬ -¥
for fiecare w succesor al lui u do
if
w nu are succesor
then valw ¬ eval(w)
else valw ¬ min{eval(x) | x este succesor al lui w}
if
valw ³ val then val ¬ valw
v ¬ w
Pentru a adauga si mai mult dinamism functiei eval, este preferabil sa investigam mai multe mutari in avans. Din pozitia u, analizand n mutari in avans, Albul va muta atunci in pozitia v data de
val ¬ -¥
for fiecare w succesor al lui u do
if
negru(w, n) ³ val then val ¬ negru(w, n)
v ¬ w
Functiile negru si alb sunt urmatoarele:
function
negru(w, n)
if
n = 0 or w
nu are succesori
then return eval(w)
return min{alb(x, n-1) | x
este succesor al lui w}
function alb(x, n)
if
n = 0 or x
nu are succesori
then return eval(x)
return max{negru(w, n-1) | w
este succesor al lui x}
Acum intelegem de ce aceasta tehnica este numita minimax: Negrul incearca sa minimizeze avantajul pe care il permite Albului, iar Albul incearca sa maximizeze avantajul pe care il poate obtine la fiecare mutare.
Tehnica minimax poate fi imbunatatita in mai multe feluri. Astfel, explorarea anumitor ramuri poate fi abandonata mai curand, daca din informatia pe care o detinem asupra lor, deducem ca ele nu mai pot influenta valoarea varfurilor situate la un nivel superior. Acesta imbunatatire se numeste retezare alfa-beta (alpha-beta pruning) si este exemplificata in Figura 9.4. Presupunand ca valorile numerice atasate varfurilor terminale sunt valorile functiei eval calculate in pozitiile respective, celelalte valori se pot calcula prin tehnica minimax, parcurgand arborele in postordine. Obtinem succesiv eval(b) = 5, eval( f ) = 6, eval(g) = 3. In acest moment stim deja ca eval(c) £ 3 si, fara sa-l mai calculam pe eval(h), obtinem valoarea eval(a) = 5. Cu alte cuvinte, la o anumita faza a explorarii am dedus ca putem abandona explorarea subarborelui cu radacina in h (il putem “reteza”).
Tehnica minimax determina in final strategia reprezentata in Figura 9.4 prin muchiile continue.
|
|
Multe probleme se pot descompune intr-o serie de subprobleme, astfel incat rezolvarea tuturor acestor subprobleme, sau a unora din ele, sa duca la rezolvarea problemei initiale. Descompunerea unei probleme complexe, in mod recursiv, in subprobleme mai simple poate fi reprezentata printr-un graf orientat. Aceasta descompunere se numeste reducerea problemei si este folosita in demonstrarea automata, integrare simbolica si, in general, in inteligenta artificiala. Intr-un graf orientat de acest tip vom permite unui varf neterminal v oarecare doua alternative. Varful v este de tip AND daca reprezinta o problema care este rezolvata doar daca toate subproblemele reprezentate de varfurile adiacente lui v sunt rezolvate. Varful v este de tip OR daca reprezinta o problema care este rezolvata doar daca cel putin o subproblema reprezentata de varfurile adiacente lui v este rezolvata. Un astfel de graf este de tip AND/OR.
De exemplu, arborele AND/OR din Figura 9.5 reprezinta reducerea problemei A. Varfurile terminale reprezinta probleme primitive, marcate ca rezolvabile (varfurile albe), sau nerezolvabile (varfurile gri). Varfurile neterminale reprezinta probleme despre care nu se stie a priori daca sunt rezolvabile sau nerezolvabile. Varful A este un varf AND (marcam aceasta prin unirea muchiilor care pleaca din A), varfurile C si D sunt varfuri OR. Sa presupunem acum ca dorim sa aflam daca problema A este rezolvabila. Deducem succesiv ca problemele C, D si A sunt rezolvabile.
|
|
Intr-un arbore oarecare AND/OR, urmatorul algoritm determina daca problema reprezentata de un varf oarecare u este rezolvabila sau nu. Un apel sol(u) are ca efect parcurgerea in postordine a subarborelui cu radacina in u si returnarea valorii true, daca si numai daca problema este rezolvabila.
function sol(v)
case
v este terminal: if v
este rezolvabil
then return
true
else return false
v este un virf AND: for fiecare
virf w adiacent lui v do
if not sol(w) then return false
return true
v este un virf OR: for
fiecare virf w adiacent lui v do
if sol(w) then
return true
return false
Ca si in cazul retezarii alfa-beta, daca in timpul explorarii se poate deduce ca un varf este rezolvabil sau nerezolvabil, se abandoneaza explorarea descendentilor sai. Printr-o modificare simpla, algoritmul sol poate afisa strategia de rezolvare a problemei reprezentate de u, adica subproblemele rezolvabile care conduc la rezolvarea problemei din u.
Cu anumite modificari, algoritmul se poate aplica asupra grafurilor AND/OR oarecare. Similar cu tehnica backtracking, explorarea se poate face atat in adancime (ca in algoritmul sol), cat si in latime.
9.1 Intr-un arbore binar de cautare, care este modul de parcurgere a varfurilor pentru a obtine lista ordonata crescator a cheilor?
9.2 Fiecarei expresii aritmetice in care apar numai operatori binari
i se poate atasa in mod natural un arbore binar. Dati exemple de parcurgere
in inordine, preordine si postordine a unui astfel de arbore. Se obtin diferite
moduri de scriere a expresiilor aritmetice. Astfel, parcurgerea in postordine
genereaza scrierea postfixata mentionata in Sectiunea 3.1.1.
9.3 Fie un arbore binar reprezentat prin
adrese, astfel incat varful i (adica
varful a carui adresa este i) este
memorat in trei locatii diferite continand:
VAL[i] = valoarea
varfului
ST[i] = adresa fiului stang
DR[i] = adresa fiului drept
(Daca se foloseste o implementare prin tablouri paralele, atunci adresele sunt indici de tablou). Presupunem ca variabila root contine adresa radacinii arborelui si ca o adresa este zero, daca si numai daca varful catre care se face trimiterea lipseste. Scrieti algoritmii de parcurgere in inordine, preordine si postordine a arborelui. La fiecare consultare afisati valoarea varfului respectiv.
Solutie: Pentru parcurgerea in inordine apelam inordine(root), inordine fiind procedura
procedure inordine(i)
if
i ¹ 0 then
inordine(ST[i])
write VAL[i]
inordine(DR[i])
9.4 Dati un algoritm care foloseste parcurgerea i) in adancime
ii) in latime pentru a afla numarul componentelor conexe ale unui graf
neorientat. In particular, puteti determina astfel daca graful este conex. Faceti
o comparatie cu algoritmul din Exercitiul 3.12.
9.5 Intr-un graf orientat, folosind
principiul parcurgerii in latime, elaborati un algoritm care gaseste cel mai
scurt ciclu care contine un anumit varf dat. In locul parcurgerii in latime,
puteti folosi parcurgerea in adancime?
9.6 Revedeti Exercitiul 8.8. Scrieti un
algoritm care gaseste inchiderea tranzitiva a unui graf orientat. Folositi
parcurgerea in adancime sau latime. Comparati algoritmul obtinut cu algoritmul
lui Warshall.
9.7 Intr-un
arbore cu radacina, elaborati un algoritm care verifica pentru doua varfuri
oarecare v si w, daca w este un
descendent al lui v. (Pentru ca
problema sa nu devina triviala, presupunem ca varfurile nu contin adresa
tatalui).
Indicatie: Orice solutie directa necesita un timp in W(n), in cazul cel mai nefavorabil, unde n este numarul varfurilor subarborelui cu radacina in v.
Iata un mod indirect de rezolvare a problemei, care este in principiu avantajos atunci cand trebuie sa verificam mai multe cazuri (perechi de varfuri) pentru acelasi arbore. Fie preord[1 .. n] si postord[1 .. n] tablourile care contin ordinea de parcurgere a varfurilor in preordine, respectiv in postordine. Pentru oricare doua varfuri v si w avem:
preord[v] < preord[w] Û w este un descendent al lui v,
sau
v este la stanga lui w in arbore
postord[v] > postord[w] Û w este un descendent al lui v,
sau
v este la dreapta lui w in arbore
Deci, w este un descendent al lui v, daca si numai daca:
preord[v] < preord[w] si postord[v] > postord[w]
Dupa ce calculam valorile preord si postord intr-un timp in Q(n), orice caz particular se poate rezolva intr-un timp in Q(1). Acest mod indirect de rezolvare ilustreaza metoda preconditionarii.
9.8 Fie A arborele partial generat de parcurgerea in adancime a grafului
neorientat conex G. Demonstrati ca,
pentru orice muchie {v, w} din G, este adevarata
urmatoarea proprietate: v este un
descendent sau un ascendent al lui w in
A.
Solutie: Daca muchiei {v, w} ii corespunde o muchie in A, atunci proprietatea este evident adevarata. Putem presupune deci ca varfurile v si w nu sunt adiacente in A. Fara a pierde din generalitate, putem considera ca v este vizitat inaintea lui w. Parcurgerea in adancime a grafului G inseamna, prin definitie, ca explorarea varfului v nu se incheie decat dupa ce a fost vizitat si varful w (tinand cont de existenta muchiei {v, w}). Deci, v este un ascendent al lui w in A.
9.9 Daca v este un varf al unui graf conex, demonstrati ca v este un punct de articulare, daca si numai daca exista doua varfuri a si b diferite de v, astfel incat orice drum care il conecteaza pe a cu b trece in mod necesar prin v.
9.10 Fie G un graf neorientat conex, dar nu si
biconex. Elaborati un algoritm pentru gasirea multimii minime de muchii care sa
fie adaugata lui G, astfel incat G sa devina biconex. Analizati algoritmul obtinut.
9.11 Fie M[1 .. n, 1 .. n]
o matrice booleana care reprezinta un labirint in forma unei table de sah. In
general, pornind dintr-un punct dat, este permis sa mergeti catre
punctele adiacente de pe aceeasi linie sau coloana. Prin punctul (i, j) se poate trece daca si numai daca M(i, j) este true. Elaborati un algoritm backtracking care gaseste un drum intre
colturile (1, 1) si (n, n), daca un astfel de drum exista.
9.12 In algoritmul perm de generare a permutarilor, inlocuiti
“utilizeaza(T)” cu “write T ” si scrieti
rezultatul afisat de perm(1), pentru n = 3. Faceti apoi
acelasi lucru, presupunand ca tabloul T este initializat cu [n, n-1, ..., 1].
9.13 (Problema submultimilor de suma data). Fie multimea de numere
pozitive W = {w1, ..., wn}
si fie M un numar pozitiv. Elaborati un algoritm backtracking care gaseste
toate submultimile lui W pentru care suma elementelor este M.
Indicatie: Fie W = {11, 13, 24, 7} si M = 31. Cel mai important lucru este cum reprezentam vectorii care vor fi varfurile arborelui generat. Iata doua moduri de reprezentare pentru solutia (11, 13, 7):
i) Prin vectorul indicilor: (1, 2, 4).
In aceasta reprezentare, vectorii solutie au lungimea variabila.
ii) Prin vectorul boolean x = (1, 1, 0, 1),
unde x[i] = 1, daca si numai daca wi
a fost selectat in solutie. De aceasta data, vectorii solutie au lungimea constanta.
9.14 Un cal este plasat in pozitia arbitrara
(i, j), pe o tabla de sah de n ´ n patrate. Concepeti
un algoritm backtracking care determina n2-1 mutari ale calului,
astfel incat fiecare pozitie de pe tabla este vizitata exact o data
(presupunand ca o astfel de secventa de mutari exista).
9.15 Gasiti un
algoritm backtracking capabil sa transforme un intreg n intr-un intreg m,
aplicand cat mai putine transformari de forma f(i) = 3i si g(i) = ëi/2û. De exemplu, 15 poate fi transformat in
4 folosind patru transformari: 4 = gfgg(15). Cum se comporta algoritmul daca este imposibil de
transformat astfel n in m ?
9.16 Modificati algoritmul rec
pentru jocul nim, astfel incat sa returneze un intreg k:
i) k = 0, daca pozitia este
de pierdere.
ii) 1 £ k £ j,
daca “a lua k bete” este o mutare de castig.
9.17 Jocul lui
Grundy seamana foarte mult cu jocul nim. Initial, pe masa se afla o singura
gramada de n bete. Cei doi jucatori
au alternativ dreptul la o mutare. O mutare consta din impartirea uneia din
gramezile existente in doua gramezi de marimi diferite (daca acest lucru nu
este posibil, adica daca toate gramezile constau din unul sau doua bete,
jucatorul pierde partida). Ca si la nim, remiza este exclusa. Gasiti un
algoritm care sa determine daca o pozitie este de castig sau de pierdere.
9.18 Tehnica minimax modeleaza eficient, dar
in acelasi timp si simplist, comportamentul unui jucator uman. Una din
presupunerile noastre a fost ca nici unul dintre jucatori nu greseste. In ce
masura ramine valabila aceasta tehnica daca admitem ca: i) jucatorii pot sa greseasca, ii)
fiecare jucator nu exclude posibilitatea ca partenerul sa faca greseli.
9.19 Daca graful obtinut prin reducerea unei
probleme are si varfuri care nu sunt de tip AND sau de tip OR,
aratati ca prin adaugarea unor varfuri fictive putem transforma acest graf intr-un
graf AND/OR.
9.20 Modificati algoritmul sol pentru a-l putea aplica
grafurilor AND/OR oarecare.
[*] O astfel de implementare poate fi gasita, de exemplu, in E. Horowitz si S. Sahni, “Fundamentals of Computer Algorithms”, Sectiunea 6.1.1.
| Previous | Table of Contents | Next |