LABORATORUL 3            BUC

Sinteza circuitelor logice complexe plecând de la funcţia logică de transfer, folosind porţile logice de bază. Circuitele XOR, XNOR, sumator fără carry in, sumator cu carry in, multiplexorul şi demultiplexorul.

Circuitul logic

            Un circuit logic este un dispozitiv care are asociate în mod convenţional un număr oarecare de intrări logice, un număr oarecare de ieşiri logice şi o funcţie de transfer care asociază fiecărei combinaţii de intrări câte o combinaţie de ieşiri. Circuitele logice pot fi implementate folosind circuite hidraulice, pneumatice, electrice şi electronice în funcţie de destinaţia acestora.

          Circuitul logic XOR

Circuitul logic XOR: Se defineşte ca fiind circuitul cu două intrări a şi b şi o ieşire q, pentru care ieşirea q este adevărată dacă şi numai dacă cele două intrări a şi b au valori de adevăr diferite.

            Tabela de adevăr pentru funcţia XOR este:

a	b	a xor b
1	1	0
1	0	1
0	1	1
0	0	0

          Circuitul logic XNOR

Circuitul logic XNOR: Se defineşte ca fiind circuitul cu două intrări a şi b şi o ieşire q, pentru care ieşirea q este adevărată dacă şi numai dacă cele două intrări a şi b au valori de adevăr echivalente.

            Tabela de adevăr pentru funcţia XNOR este:

a	b	a xnor b
1	1	1
1	0	0
0	1	0
0	0	1

          Circuitul logic sumator fără carry in

Circuitul logic sumator pe doi bits fără carry in: Se defineşte ca fiind circuitul cu două intrări a şi b şi două ieşiri p şi q, pentru care ieşirea p este echivalentă cu ( a xor b ) şi ieşirea q este echivalentă cu ( a and b ). Ieşirea p se cheamă suma celor două intrări şi ieşirea q se cheamă depăşirea sau carry out.

            Tabela de adevăr pentru funcţia circuitului logic sumator fără carry in este:

a	b	p	q
1	1	0	1
1	0	1	0
0	1	1	0
0	0	0	0

            În baza 10 ca şi în baza 2 avem 0+0=0, 1+0=1, 0+1=1 dar 1₂+1₂=10₂, ca şi cum am zice că 5₁₀+5₁₀=10₁₀, adică rezultatul sumei va fi reprezentat pe doi digits, cel de al doilea reprezintă suma propriu zisă în timp ce primul reprezintă depăşirea, deci 1₂+1₂=10₂ sau 5₁₀+7₁₀=12₁₀.

            Matematic scriem:         a+b=p+q*2

          Circuitul logic sumator cu carry in

Circuitul logic sumator pe doi bits cu carry in: Se defineşte ca fiind circuitul cu trei intrări a, b şi c şi două ieşiri p şi q, pentru care putem scrie: a+b+c=p+q*2

            Tabela de adevăr pentru funcţia circuitului logic sumator cu carry in este:

a	b	c	p	q
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

            Într-un lanţ de sumatoare pe doi bits cu carry in, intrarea c (carry in) a unui sumator oarecare coincide cu ieşirea q (carry out) a sumatorului anterior. Cu ajutorul unui lanţ de n sumatoare cu carry in se poate calcula suma în baza doi a două numere reprezentate pe n bits.

          Multiplexorul pe doi bits

Multiplexorul pe doi bits: Este circuitul cu trei intrări a, b, c (două de date a şi b şi una de comandă c) şi o ieşire q care conform funcţiei de transfer este echivalentă cu intrarea de date a dacă intrarea de comandă c este falsă şi este echivalentă cu intrarea de date b dacă intrarea de comandă c este adevărată.

            Tabela de adevăr pentru funcţia circuitului logic multiplexor este:

c	a	b	q
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	1
1	1	0	0
1	1	1	1

          Simbolurile porţilor logice

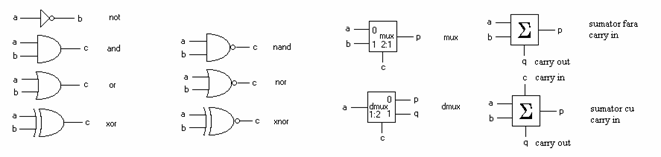
          Sinteza circuitului logic XOR prin disjuncţie de mintermi

Etapa 1: Se adaugă la tabela de adevăr coloanele corespunzătoare intrărilor negate.

a	not a	b	not b	a xor b
0	1	0	1	0
0	1	1	0	1
1	0	0	1	1
1	0	1	0	0

            Se desenează circuitul care generează cele patru intrări a, not a, b, not b.

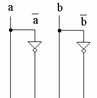
Etapa 2: Se tratează pe rând cazurile pentru care rezultatul a xor b este 1, care sunt două (doi mintermi):

a	not a	b	not b	a xor b
0	1	1	0	1
1	0	0	1	1

            Primul minterm este ((not a) and b) deoarece conjuncţia a două variabile este adevărata doar atunci când cele două variabile sunt adevărate şi deci am ales din table variabilele (not a) şi (b).

            Putem astfel desena:

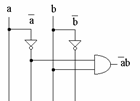
            Al doilea minterm este (a and (not b)), pe acelaşi criteriu.

            Putem astfel desena:

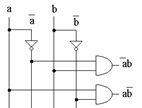
Etapa 3: Avem cei doi mintermi şi facem disjuncţia acestora: ((not a) and b) or (a and (not b))

            Putem astfel desena:

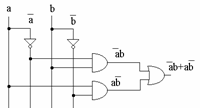
          Sinteza circuitului logic XOR prin conjuncţie de maxtermi

Etapa 1: Se adaugă la tabela de adevăr coloanele corespunzătoare intrărilor negate.

a	not a	b	not b	a xor b
0	1	0	1	0
0	1	1	0	1
1	0	0	1	1
1	0	1	0	0

            Se desenează circuitul care generează cele patru intrări a, not a, b, not b.

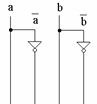
Etapa 2: Se tratează pe rând cazurile pentru care rezultatul a xor b este 0, care sunt două (doi maxtermi):

a	not a	b	not b	a xor b
0	1	0	1	0
1	0	1	0	0

            Primul maxterm este (a or b) deoarece disjuncţia a două variabile este falsă doar atunci când cele două variabile sunt false şi deci am ales din table variabilele (a) şi (b).

            Putem astfel desena:

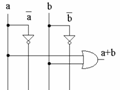
            Al doilea maxterm este ((not a) or (not b)), pe acelaşi criteriu.

            Putem astfel desena:

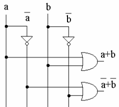
Etapa 4: Avem cei doi maxtermi şi facem conjuncţia acestora: (a or b) and ((not a) or (not b))

            Putem astfel desena:

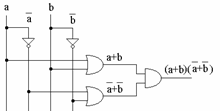
            Cele două circuite, chiar dacă sunt diferite, au aceiaşi funcţie de transfer, adică pentru intrări echivalente generează ieşiri echivalente.

EXERCIŢII

1. Faceţi verificarea celor două exemple de mai sus aplicând valori concrete la intrările celor două circuite rezultate. Se verifică toate situaţiile ?

2. Faceţi sinteza circuitelor XNOR, sumator fără carry in, sumator cu carry in şi multiplexorul pe doi bits folosind pe rând ambele metode de sinteză.

3. Circuitul logic multiplexor pe doi bits poate fi sintetizat folosind in total numai patru porţi logice. Pentru a obţine schema minimală deduceţi funcţia de transfer plecând de la tabela funcţiei de transfer (sau de la circuitul obţinut la exerciţiul anterior), faceţi minimizarea acesteia şi apoi deduceţi direct circuitul echivalent minimal.