
| Previous | Table of Contents | Next |
3. Structuri elementare de date
3.1 Liste
3.1.1 Stive
3.1.2 Cozi
3.2 Grafuri
3.3 Arbori cu radacina
3.4 Heap-uri
3.5 Structuri de multimi disjuncte
3.6 Exercitii
Inainte de a elabora un algoritm, trebuie sa ne gandim la modul in care reprezentam datele. In acest capitol vom trece in revista structurile fundamentale de date cu care vom opera. Presupunem in continuare ca sunteti deja familiarizati cu notiunile de fisier, tablou, lista, graf, arbore si ne vom concentra mai ales pe prezentarea unor concepte mai particulare: heap-uri si structuri de multimi disjuncte.
O lista este o colectie de elemente de informatie (noduri) aranjate intr-o anumita ordine. Lungimea unei liste este numarul de noduri din lista. Structura corespunzatoare de date trebuie sa ne permita sa determinam eficient care este primul/ultimul nod in structura si care este predecesorul/succesorul (daca exista) unui nod dat. Iata cum arata cea mai simpla lista, lista liniara:

O lista circulara este o lista in care, dupa ultimul nod, urmeaza primul, deci fiecare nod are succesor si predecesor.
Operatii curente care se fac in liste sunt: inserarea unui nod, stergerea (extragerea) unui nod, concatenarea unor liste, numararea elementelor unei liste etc. Implementarea unei liste se poate face in principal in doua moduri:
Listele implementate inlantuit pot fi reprezentate cel mai simplu prin tablouri. In acest caz, adresele sunt de fapt indici de tablou. O alternativa este sa folosim tablouri paralele: sa memoram informatia fiecarui nod (valoarea) intr-o locatie VAL[i] a tabloului VAL[1 .. n], iar adresa (indicele) nodului sau succesor intr-o locatie LINK[i] a tabloului LINK[1 .. n]. Indicele de tablou al locatiei primului nod este memorat in variabila head. Vom conveni ca, pentru cazul listei vide, sa avem head = 0. Convenim de asemenea ca LINK[ultimul nod din lista] = 0. Atunci, VAL[head] va contine informatia primului nod al listei, LINK[head] adresa celui de-al doilea nod, VAL[LINK[head]] informatia din al doilea nod, LINK[LINK[head]] adresa celui de-al treilea nod etc.
Acest mod de reprezentare este simplu dar, la o analiza mai atenta, apare o problema esentiala: cea a gestionarii locatiilor libere. O solutie eleganta este sa reprezentam locatiile libere tot sub forma unei liste inlantuite. Atunci, stergerea unui nod din lista initiala implica inserarea sa in lista cu locatii libere, iar inserarea unui nod in lista initiala implica stergerea sa din lista cu locatii libere. Aspectul cel mai interesant este ca, pentru implementarea listei de locatii libere, putem folosi aceleasi tablouri. Avem nevoie de o alta variabila, freehead, care va contine indicele primei locatii libere din VAL si LINK. Folosim aceleasi conventii: daca freehead = 0 inseamna ca nu mai avem locatii libere, iar LINK[ultima locatie libera] = 0.
Vom descrie in continuare doua tipuri de liste particulare foarte des folosite.
O stiva (stack) este o lista liniara cu proprietatea ca operatiile de inserare/extragere a nodurilor se fac in/din coada listei. Daca nodurile A, B, C, D sunt inserate intr-o stiva in aceasta ordine, atunci primul nod care poate fi extras este D. In mod echivalent, spunem ca ultimul nod inserat va fi si primul sters. Din acest motiv, stivele se mai numesc si liste LIFO (Last In First Out), sau liste pushdown.
Cel mai natural mod de reprezentare pentru o stiva este implementarea secventiala intr-un tablou S[1 .. n], unde n este numarul maxim de noduri. Primul nod va fi memorat in S[1], al doilea in S[2], iar ultimul in S[top], unde top este o variabila care contine adresa (indicele) ultimului nod inserat. Initial, cand stiva este vida, avem top = 0. Iata algoritmii de inserare si de stergere (extragere) a unui nod:
function push(x, S[1 .. n])
{adauga nodul x in stiva}
if
top ³ n then return “stiva plina”
top
¬ top+1
S[top] ¬ x
return “succes”
function pop(S[1 .. n])
{sterge ultimul nod inserat din stiva
si il returneaza}
if
top £ 0 then return “stiva vida”
x
¬ S[top]
top
¬ top-1
return
x
Cei doi algoritmi necesita timp constant, deci nu depind de marimea stivei.
Vom da un exemplu elementar de utilizare a unei stive. Daca avem de calculat expresia aritmetica
5*(((9+8)*(4*6))+7)
putem folosi o stiva pentru a memora rezultatele intermediare. Intr-o scriere simplificata, iata cum se poate calcula expresia de mai sus:
push(5); push(9); push(8); push(pop + pop); push(4); push(6);
push(pop * pop); push(pop * pop); push(7); push(pop + pop);
push(pop * pop); write (pop);
Observam ca, pentru a efectua o operatie aritmetica, trebuie ca operanzii sa fie deja in stiva atunci cand intalnim operatorul. Orice expresie aritmetica poate fi transformata astfel incat sa indeplineasca aceasta conditie. Prin aceasta transformare se obtine binecunoscuta notatie postfixata (sau poloneza inversa), care se bucura de o proprietate remarcabila: nu sunt necesare paranteze pentru a indica ordinea operatiilor. Pentru exemplul de mai sus, notatia postfixata este:
5 9 8 + 4 6 * * 7 + *
O coada (queue) este o lista liniara in care inserarile se fac doar in capul listei, iar extragerile doar din coada listei. Cozile se numesc si liste FIFO (First In First Out).
O reprezentare secventiala interesanta pentru o coada se obtine prin utilizarea unui tablou C[0 .. n-1], pe care il tratam ca si cum ar fi circular: dupa locatia C[n-1] urmeaza locatia C[0]. Fie tail variabila care contine indicele locatiei predecesoare primei locatii ocupate si fie head variabila care contine indicele locatiei ocupate ultima oara. Variabilele head si tail au aceeasi valoare atunci si numai atunci cand coada este vida. Initial, avem head = tail = 0. Inserarea si stergerea (extragerea) unui nod necesita timp constant.
function insert-queue(x, C[0
.. n-1])
{adauga nodul x in capul cozii}
head
¬ (head+1) mod n
if
head = tail then return “coada
plina”
C[head] ¬ x
return
“succes”
function delete-queue(C[0 .. n-1])
{sterge nodul din coada listei si il
returneaza}
if
head = tail then return “coada
vida”
tail
¬ (tail+1) mod n
x
¬ C[tail]
return
x
Este surprinzator faptul ca testul de coada vida este acelasi cu testul de coada plina. Daca am folosi toate cele n locatii, atunci nu am putea distinge intre situatia de “coada plina” si cea de “coada vida”, deoarece in ambele situatii am avea head = tail. In consecinta, se folosesc efectiv numai n-1 locatii din cele n ale tabloului C, deci se pot implementa astfel cozi cu cel mult n-1 noduri.
Un graf este o pereche G = <V, M>, unde V este o multime de varfuri, iar M Í V ´ V este o multime de muchii. O muchie de la varful a la varful b este notata cu perechea ordonata (a, b), daca graful este orientat, si cu multimea {a, b}, daca graful este neorientat. In cele ce urmeaza vom presupune ca varfurile a si b sunt diferite. Doua varfuri unite printr-o muchie se numesc adiacente. Un drum este o succesiune de muchii de forma
(a1, a2),
(a2, a3), ..., (an-1, an)
sau de forma
{a1, a2},
{a2, a3}, ..., {an-1, an}
dupa cum graful este orientat sau neorientat. Lungimea drumului este egala cu numarul muchiilor care il constituie. Un drum simplu este un drum in care nici un varf nu se repeta. Un ciclu este un drum care este simplu, cu exceptia primului si ultimului varf, care coincid. Un graf aciclic este un graf fara cicluri. Un subgraf al lui G este un graf <V', M'>, unde V' Í V, iar M' este formata din muchiile din M care unesc varfuri din V'. Un graf partial este un graf <V, M">, unde M" Í M.
Un graf neorientat este conex, daca intre oricare doua varfuri exista un drum. Pentru grafuri orientate, aceasta notiune este intarita: un graf orientat este tare conex, daca intre oricare doua varfuri i si j exista un drum de la i la j si un drum de la j la i.
In cazul unui graf neconex, se pune problema determinarii componentelor sale conexe. O componenta conexa este un subgraf conex maximal, adica un subgraf conex in care nici un varf din subgraf nu este unit cu unul din afara printr-o muchie a grafului initial. Impartirea unui graf G = <V, M> in componentele sale conexe determina o partitie a lui V si una a lui M.
Un arbore este un graf neorientat aciclic conex. Sau, echivalent, un arbore este un graf neorientat in care exista exact un drum intre oricare doua varfuri[*] . Un graf partial care este arbore se numeste arbore partial.
Varfurilor unui graf li se pot atasa informatii numite uneori valori, iar muchiilor li se pot atasa informatii numite uneori lungimi sau costuri.
Exista cel putin trei moduri evidente de reprezentare ale unui graf:
|
Figura 3.1 Un arbore cu radacina. |
Fie G un graf orientat. G este un arbore cu radacina r, daca exista in G un varf r din care oricare alt varf poate fi ajuns printr-un drum unic.
Definitia este valabila si pentru cazul unui graf neorientat, alegerea unei radacini fiind insa in acest caz arbitrara: orice arbore este un arbore cu radacina, iar radacina poate fi fixata in oricare varf al sau. Aceasta, deoarece dintr-un varf oarecare se poate ajunge in oricare alt varf printr-un drum unic.
Cand nu va fi pericol de confuzie, vom folosi termenul “arbore”, in loc de termenul corect “arbore cu radacina”. Cel mai intuitiv este sa reprezentam un arbore cu radacina, ca pe un arbore propriu-zis. In Figura 3.1, vom spune ca beta este tatal lui delta si fiul lui alpha, ca beta si gamma sunt frati, ca delta este un descendent al lui alpha, iar alpha este un ascendent al lui delta. Un varf terminal este un varf fara descendenti. Varfurile care nu sunt terminale sunt neterminale. De multe ori, vom considera ca exista o ordonare a descendentilor aceluiasi parinte: beta este situat la stanga lui gamma, adica beta este fratele mai varstnic al lui gamma.
Orice varf al unui arbore cu radacina este radacina unui subarbore constand din varful respectiv si toti descendentii sai. O multime de arbori disjuncti formeaza o padure.
Intr-un arbore cu radacina vom adopta urmatoarele notatii. Adancimea unui varf este lungimea drumului dintre radacina si acest varf; inaltimea unui varf este lungimea celui mai lung drum dintre acest varf si un varf terminal; inaltimea arborelui este inaltimea radacinii; nivelul unui varf este inaltimea arborelui, minus adancimea acestui varf.
Reprezentarea unui arbore cu radacina se poate face prin adrese, ca si in cazul listelor inlantuite. Fiecare varf va fi memorat in trei locatii diferite, reprezentand informatia propriu-zisa a varfului (valoarea varfului), adresa celui mai varstnic fiu si adresa urmatorului frate. Pastrand analogia cu listele inlantuite, daca se cunoaste de la inceput numarul maxim de varfuri, atunci implementarea arborilor cu radacina se poate face prin tablouri paralele.
Daca fiecare varf al unui arbore cu radacina are pana la n fii, arborele respectiv este n-ar. Un arbore binar poate fi reprezentat prin adrese, ca in Figura 3.2. Observam ca pozitiile pe care le ocupa cei doi fii ai unui varf sunt semnificative: lui a ii lipseste fiul drept, iar b este fiul stang al lui a.
|
Figura 3.2 Reprezentarea prin adrese a unui arbore binar. |
Intr-un arbore binar, numarul maxim de varfuri de adancime k este 2k. Un arbore binar de inaltime i are cel mult 2i+1-1 varfuri, iar daca are exact 2i+1-1 varfuri, se numeste arbore plin. Varfurile unui arbore plin se numeroteaza in ordinea adancimii. Pentru aceeasi adancime, numerotarea se face in arbore de la stanga la dreapta (Figura 3.3).
|
Figura 3.3 Numerotarea varfurilor intr-un arbore binar de inaltime 3. |
Un arbore binar cu n varfuri si de inaltime i este complet, daca se obtine din arborele binar plin de inaltime i, prin eliminarea, daca este cazul, a varfurilor numerotate cu n+1, n+2, …, 2i+1-1. Acest tip de arbore se poate reprezenta secvential folosind un tablou T, punand varfurile de adancime k, de la stanga la dreapta, in pozitiile T[2k], T[2k+1], …, T[2k+1-1] (cu posibila exceptie a nivelului 0, care poate fi incomplet). De exemplu, Figura 3.4 exemplifica cum poate fi reprezentat un arbore binar complet cu zece varfuri, obtinut din arborele plin din Figura 3.3, prin eliminarea varfurilor 11, 12, 13, 14 si 15. Tatal unui varf reprezentat in T[i], i > 1, se afla in T[i div 2]. Fiii unui varf reprezentat in T[i] se afla, daca exista, in T[2i] si T[2i+1].
|
Figura 3.4 Un arbore binar complet. |
Facem acum o scurta incursiune in matematica elementara, pentru a stabili cateva
rezultate de care vom avea nevoie in capitolele urmatoare. Pentru un numar real
oarecare x, definim
ëxû = max{n ï n £ x, n este intreg} si éxù = min{n ï n ³ x, n este intreg}
Puteti demonstra cu usurinta urmatoarele proprietati:
i) x-1 < ëxû £ x £ éxù < x+1
pentru orice x real
ii) ën/2û + én/2ù = n
pentru orice n intreg
iii) één/aù/bù = én/abù
si ëën/aû/bû = ën/abû
pentru orice n, a, b intregi (a, b ¹ 0)
iv) ën/mû = é(n-m+1)/mù
si én/mù = ë(n+m-1)/mû
pentru orice numere intregi pozitive n
si m
In fine, aratati ca un arbore binar complet cu n varfuri are inaltimea ëlg nû.
Un heap (in traducere aproximativa, “gramada ordonata”) este un arbore binar complet, cu urmatoarea proprietate, numita proprietate de heap: valoarea fiecarui varf este mai mare sau egala cu valoarea fiecarui fiu al sau. Figura 3.5 prezinta un exemplu de heap.
|
Figura 3.5 Un heap. |
Acelasi heap poate fi reprezentat secvential prin urmatorul tablou:
|
10 |
7 |
9 |
4 |
7 |
5 |
2 |
2 |
1 |
6 |
|
T[1] |
T[2] |
T[3] |
T[4] |
T[5] |
T[6] |
T[7] |
T[8] |
T[9] |
T[10] |
Caracteristica de baza a acestei structuri de data este ca modificarea valorii unui varf se face foarte eficient, pastrandu-se proprietatea de heap. Daca valoarea unui varf creste, astfel incat depaseste valoarea tatalui, este suficient sa schimbam intre ele aceste doua valori si sa continuam procedeul in mod ascendent, pana cand proprietatea de heap este restabilita. Vom spune ca valoarea modificata a fost filtrata ( percolated ) catre noua sa pozitie. Daca, dimpotriva, valoarea varfului scade, astfel incat devine mai mica decat valoarea cel putin a unui fiu, este suficient sa schimbam intre ele valoarea modificata cu cea mai mare valoare a fiiilor, apoi sa continuam procesul in mod descendent, pana cand proprietatea de heap este restabilita. Vom spune ca valoarea modificata a fost cernuta (sifted down) catre noua sa pozitie. Urmatoarele proceduri descriu formal operatiunea de modificare a valorii unui varf intr-un heap.
procedure alter-heap(T[1 .. n], i, v)
{T[1
.. n] este un heap; lui T[i],
1 £ i £ n, i se atribuie
valoarea v si proprietatea de
heap este restabilita}
x
¬ T[i]
T[i] ¬ v
if
v < x then sift-down(T, i)
else percolate(T, i)
procedure sift-down(T[1 .. n], i)
{se cerne valoarea din T[i]}
k
¬ i
repeat
j ¬ k
{gaseste fiul cu valoarea
cea mai mare}
if 2j £ n and T[2j] > T[k] then
k ¬ 2j
if 2j < n and
T[2j+1] > T[k]
then k ¬ 2j+1
interschimba T[ j]
si T[k]
until
j = k
procedure percolate(T[1 .. n], i)
{se filtreaza valoarea din T[i]}
k
¬ i
repeat
j ¬ k
if j > 1 and T[
j div 2] < T[k] then
k ¬ j div 2
interschimbaT[ j] si T[k]
until
j = k
Heap-ul este structura de date ideala pentru determinarea si extragerea maximului dintr-o multime, pentru inserarea unui varf, pentru modificarea valorii unui varf. Sunt exact operatiile de care avem nevoie pentru a implementa o lista dinamica de prioritati: valoarea unui varf va da prioritatea evenimentului corespunzator. Evenimentul cu prioritatea cea mai mare se va afla mereu la radacina heap-ului, iar prioritatea unui eveniment poate fi modificata in mod dinamic. Algoritmii care efectueaza aceste operatii sunt:
function find-max(T[1 .. n])
{returneaza elementul cel mai mare
din heap-ul T}
return
T[1]
procedure delete-max(T[1 .. n])
{sterge elementul cel mai mare din
heap-ul T}
T[1]
¬ T[n]
sift-down(T[1
.. n-1], 1)
procedure insert(T[1 .. n], v)
{insereaza un element cu valoarea v in heap-ul T
si restabileste proprietatea de heap}
T[n+1] ¬ v
percolate(T[1 .. n+1], n+1)
Ramane de vazut cum putem forma un heap pornind de la tabloul neordonat T[1 .. n]. O solutie evidenta este de a porni cu un heap vid si sa adaugam elementele unul cate unul.
procedure slow-make-heap(T[1 .. n])
{formeaza, in mod ineficient, din T un heap}
for
i ¬ 2 to n do
percolate(T[1 .. i], i)
Solutia nu este eficienta si, in Capitolul 5 , vom reveni asupra acestui lucru. Exista din fericire un algoritm mai inteligent, care lucreaza in timp liniar, dupa cum vom demonstra tot in Capitolul 5 .
procedure make-heap(T[1 .. n])
{formeaza din T un heap}
for
i ¬ (n div 2) downto 1 do sift-down[T,
i]
Ne reamintim ca in T[n div 2] se afla tatal varfului din T[n]. Pentru a intelege cum lucreaza aceasta procedura, sa presupunem ca pornim de la tabloul:
|
1 |
6 |
9 |
2 |
7 |
5 |
2 |
7 |
4 |
10 |
care corespunde arborelui:
|
|
Mai intai formam heap-uri din subarborii cu radacina la nivelul 1, aplicand procedura sift-down radacinilor respective:
|
|
Dupa acest pas, tabloul T devine:
|
1 |
6 |
9 |
7 |
10 |
5 |
2 |
2 |
4 |
7 |
Subarborii de la urmatorul nivel sunt apoi transformati si ei in heap-uri. Astfel, subarborele
|
|
se transforma succesiv in:
|
|
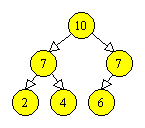 |
Subarborele de nivel 2 din dreapta este deja heap. Dupa acest pas, tabloul T devine:
|
1 |
10 |
9 |
7 |
7 |
5 |
2 |
2 |
4 |
6 |
Urmeaza apoi sa repetam procedeul si pentru nivelul 3, obtinand in final heap-ul din Figura 3.5.
Un min-heap este un heap in care proprietatea de heap este inversata: valoarea fiecarui varf este mai mica sau egala cu valoarea fiecarui fiu al sau. Evident, radacina unui min-heap va contine in acest caz cel mai mic element al heap-ului. In mod corespunzator, se modifica si celelalte proceduri de manipulare a heap-ului.
Chiar daca heap-ul este o structura de date foarte atractiva, exista totusi si operatii care nu pot fi efectuate eficient intr-un heap. O astfel de operatie este, de exemplu, gasirea unui varf avand o anumita valoare data.
Conceptul de heap poate fi imbunatatit in mai multe feluri. Astfel, pentru aplicatii in care se foloseste mai des procedura percolate decat procedura sift-down, renteaza ca un varf neterminal sa aiba mai mult de doi fii. Aceasta accelereaza procedura percolate. Si un astfel de heap poate fi implementat secvential.
Heap-ul este o structura de date cu numeroase aplicatii, inclusiv o remarcabila tehnica de sortare, numita heapsort.
procedure heapsort(T[1 .. n])
{sorteaza tabloul T}
make-heap(T)
for
i ¬ n downto 2 do
interschimba T[1] si T[i]
sift-down(T[1 .. i-1], 1)
Structura de heap a fost introdusa (Williams, 1964) tocmai ca instrument pentru acest algoritm de sortare.
Sa presupunem ca avem N elemente, numerotate de la 1 la N. Numerele care identifica elementele pot fi, de exemplu, indici intr-un tablou unde sunt memorate numele elementelor. Fie o partitie a acestor N elemente, formata din submultimi doua cate doua disjuncte: S1, S2, … . Ne intereseaza sa rezolvam doua probleme:
i) Cum sa obtinem reuniunea a doua submultimi, Si È Sj.
ii) Cum sa gasim submultimea care contine un element dat.
Avem nevoie de o structura de date care sa permita rezolvarea eficienta a acestor probleme.
Deoarece submultimile sunt doua cate doua disjuncte, putem alege ca eticheta pentru o submultime oricare element al ei. Vom conveni pentru inceput ca elementul minim al unei multimi sa fie eticheta multimii respective. Astfel, multimea {3, 5, 2, 8} va fi numita “multimea 2”.
Vom aloca tabloul set[1 .. N], in care fiecarei locatii set[i] i se atribuie eticheta submultimii care contine elementul i. Avem atunci proprietatea: set[i] £ i, pentru 1 £ i £ N.
Presupunem ca, initial, fiecare element formeaza o submultime, adica set[i] = i, pentru 1 £ i £ N. Problemele i) si ii) se pot rezolva prin urmatorii algoritmi:
function find1(x)
{returneaza eticheta multimii care il
contine pe x}
return
set[x]
procedure merge1(a, b)
{fuzioneaza multimile etichetate cu a si b}
i
¬ a;
j ¬ b
if
i > j then interschimba i si j
for
k ¬ j to N do
if set[k] = j
then set[k] ¬ i
Daca consultarea sau modificarea unui element dintr-un tablou conteaza ca o operatie elementara, atunci se poate demonstra (Exercitiul 3.7) ca o serie de n operatii merge1 si find1 necesita, pentru cazul cel mai nefavorabil si pornind de la starea initiala, un timp in ordinul lui n2.
Incercam sa imbunatatim acesti algoritmi. Folosind in continuare acelasi tablou, vom reprezenta fiecare multime ca un arbore cu radacina ”inversat”. Adoptam urmatoarea tehnica: daca set[i] = i, atunci i este atat eticheta unei multimi, cat si radacina arborelui corespunzator; daca set[i] = j ¹ i, atunci j este tatal lui i intr-un arbore. De exemplu, tabloul:
| 1 | 2 | 3 | 2 | 1 | 3 | 4 | 3 | 3 | 4 |
| set[1] | set[2] | ... | set[10] |
reprezinta arborii:
|
|
care, la randul lor, reprezinta multimile {1,5}, {2,4,7,10} si {3,6,8,9}. Pentru a fuziona doua multimi, trebuie acum sa modificam doar o singura valoare in tablou; pe de alta parte, este mai dificil sa gasim multimea careia ii apartine un element dat.
function find2(x)
{returneaza eticheta multimii care il
contine pe x}
i
¬ x
while
set[i] ¹ i
do i ¬ set[i]
return
i
procedure merge2(a, b)
{fuzioneaza multimile etichetate cu a si b}
if
a < b then set[b] ¬ a
else set[a] ¬ b
O serie de n operatii find2 si merge2 necesita, pentru cazul cel mai nefavorabil si pornind de la starea initiala, un timp tot in ordinul lui n2 (Exercitiul 3.7). Deci, deocamdata, nu am castigat nimic fata de prima varianta a acestor algoritmi. Aceasta deoarece dupa k apeluri ale lui merge2, se poate sa ajungem la un arbore de inaltime k, astfel incat un apel ulterior al lui find2 sa ne puna in situatia de a parcurge k muchii pana la radacina.
Pana acum am ales (arbitrar) ca elementul minim sa fie eticheta unei multimi. Cand fuzionam doi arbori de inaltime h1 si respectiv h2, este bine sa facem astfel incat radacina arborelui de inaltime mai mica sa devina fiu al celeilalte radacini. Atunci, inaltimea arborelui rezultat va fi max(h1, h2), daca h1 ¹ h2, sau h1+1, daca h1 = h2. Vom numi aceasta tehnica regula de ponderare. Aplicarea ei implica renuntarea la conventia ca elementul minim sa fie eticheta multimii respective. Avantajul este ca inaltimea arborilor nu mai creste atat de rapid. Putem demonstra (Exercitiul 3.9) ca folosind regula de ponderare, dupa un numar arbitrar de fuzionari, pornind de la starea initiala, un arbore avand k varfuri va avea inaltimea maxima ëlg kû.
Inaltimea arborilor poate fi memorata intr-un tablou H[1 .. N], astfel incat H[i] sa contina inaltimea varfului i in arborele sau curent. In particular, daca a este eticheta unei multimi, H[a] va contine inaltimea arborelui corespunzator. Initial, H[i] = 0 pentru 1 £ i £ N. Algoritmul find2 ramane valabil, dar vom modifica algoritmul de fuzionare.
procedure merge3(a, b)
{fuzioneaza multimile etichetate cu a si b;
presupunem ca a ¹
b}
if
H[a]
= H[b]
then H[a] ¬ H[a]+1
set[b] ¬ a
else if H[a] > H[b]
then set[b]
¬ a
else set[a]
¬ b
O serie de n operatii find2 si merge3 necesita, pentru cazul cel mai nefavorabil si pornind de la starea initiala, un timp in ordinul lui n log n.
Continuam cu imbunatatirile, modificand algoritmul find2. Vom folosi tehnica comprimarii drumului, care consta in urmatoarele. Presupunand ca avem de determinat multimea care il contine pe x, traversam (conform cu find2) muchiile care conduc spre radacina arborelui. Cunoscand radacina, traversam aceleasi muchii din nou, modificand acum fiecare varf intalnit in cale astfel incat sa contina direct adresa radacinii. Folosind tehnica comprimarii drumului, nu mai este adevarat ca inaltimea unui arbore cu radacina a este data de H[a]. Totusi, H[a] reprezinta in acest caz o limita superioara a inaltimii si procedura merge3 ramane, cu aceasta observatie, valabila. Algoritmul find2 devine:
function find3(x)
{returneaza eticheta multimii care il
contine pe x}
r
¬ x
while
set[r] ¹ r
do r ¬ set[r]
{r este radacina arborelui}
i
¬ x
while
i ¹ r do
j ¬ set[i]
set[i] ¬ r
i ¬ j
return
r
De exemplu, executand operatia find3(20) asupra arborelui din Figura 3.6a, obtinem arborele din Figura 3.6b.
|
Figura 3.6 Comprimarea drumului. |
Algoritmii find3 si merge3 sunt o varianta considerabil imbunatatita a procedurilor de tip find si merge. O serie de n operatii find3 si merge3 necesita, pentru cazul cel mai nefavorabil si pornind de la starea initiala, un timp in ordinul lui n lg* N, unde lg* este definit astfel:
![]()
Demonstrarea acestei afirmatii este laborioasa si nu o vom prezenta aici. Functia lg* creste extrem de incet: lg* N £ 5 pentru orice N £ 65536 si lg* N £ 6 pentru orice N £ 265536. Deoarece numarul atomilor universului observabil este estimat la aproximativ 1080, ceea ce este mult mai putin decat 265536, vom intalni foarte rar o valoare a lui N pentru care lg* N > 6.
De acum incolo, atunci cand vom aplica procedurile find3 si merge3 asupra unor multimi disjuncte de elemente, vom spune ca folosim o structura de multimi disjuncte.
O importanta aplicatie practica a structurilor de multimi disjuncte este verificarea eficienta a conexitatii unui graf (Exercitiul 3.12).
3.1 Scrieti algoritmii de inserare si de stergere a unui nod pentru o stiva implementata prin tehnica tablourilor paralele.
3 .2 Fie G un graf neorientat cu n
varfuri, n ³ 2. Demonstrati echivalenta
urmatoarelor propozitii care caracterizeaza un arbore:
i) G este conex si aciclic.
ii) G este aciclic si are n-1 muchii.
iii) G este conex si are n-1 muchii.
iv) G este aciclic si, adaugandu-se o singura muchie intre oricare doua varfuri neadiacente, se creaza exact un ciclu.
v) G este conex si, daca se suprima o muchie oarecare, nu mai este conex.
vi) Oricare doua varfuri din G sunt unite printr-un drum unic.
3.3 Elaborati si
implementati un algoritm de evaluare a expresiilor aritmetice postfixate.
3.4 De ce procedura percolate este mai eficienta daca admitem ca un varf neterminal
poate avea mai mult de doi fii?
3.5 Fie T[1 .. 12] un tablou, astfel incat T[i] = i, pentru i < 12. Determinati starea tabloului dupa fiecare din
urmatoarele apeluri de procedura, aplicate succesiv:
make-heap(T); alter-heap(T, 12, 10); alter-heap(T, 1, 6); alter-heap(T, 5, 6)
3.6 Implementati
un model de simulare a unei liste dinamice de prioritati folosind structura de
heap.
3.7 In situatia in care, consultarea sau
modificarea unui element din tablou conteaza ca o operatie elementara,
demonstrati ca timpul de executie necesar pentru o secventa de n operatii find1 si merge1, pornind
din starea initiala si pentru cazul cel mai nefavorabil, este in ordinul lui n2. Demonstrati aceeasi proprietate
pentru find2 si merge2.
Solutie: find1 necesita un timp constant si cel mai nefavorabil caz il reprezinta secventa:
merge1(N, N-1); find1(N)
merge1(N-1, N-2); find1(N)
…
merge1(N-n+1, N-n); find1(N)
In aceasta secventa, merge1(N-i+1, N-i) necesita un timp in ordinul lui i. Timpul total este in ordinul lui 1+2+…+n = n(n+1)/2, deci in ordinul lui n2. Simetric, merge2 necesita un timp constant si cel mai nefavorabil caz il reprezinta secventa:
merge2(N, N-1); find2(N)
merge2(N-1, N-2); find2(N),
…
merge2(N-n+1, N-n); find2(N)
in care find2(i) necesita un timp in ordinul lui i etc.
3.8 De ce am presupus in procedura merge3 ca a ¹ b?
3.9 Demonstrati prin inductie ca,
folosind regula de ponderare (procedura merge3),
un arbore cu k varfuri va avea dupa
un numar arbitrar de fuzionari si pornind de la starea initiala, inaltimea
maxima ëlg kû.
Solutie: Proprietatea este adevarata pentru k = 1. Presupunem ca proprietatea este adevarata pentru i £ k-1 si demonstram ca este adevarata si pentru k.
Fie T arborele (cu k varfuri si de inaltime h) rezultat din aplicarea procedurii merge3 asupra arborilor T1 (cu m varfuri si de inaltime h1) si T2 (cu k-m varfuri si de inaltime h2). Se observa ca cel putin unul din arborii T1 si T2 are cel mult k/2 varfuri, deoarece este imposibil sa avem m > k/2 si k-m > k/2. Presupunand ca T1 are cel mult k/2 varfuri, avem doua posibilitati:
i) h1 ¹ h2 Þ h £ ëlg (k-m)û £ ëlg kû
ii) h1 = h2 Þ h = h1+1 £ ëlg mû+1 £ ëlg (k/2)û+1 = ëlg kû
3.10 Demonstrati ca o serie de n operatii find2 si merge3 necesita,
pentru cazul cel mai nefavorabil si pornind de la starea initiala, un timp in
ordinul lui n log n.
Indicatie: Tineti cont de Exercitiul 3.9 si aratati ca timpul este in ordinul lui n lg n. Aratati apoi ca baza logaritmului poate fi oarecare, ordinul timpului fiind n log n.
3.11 In locul regulii de ponderare, putem
adopta urmatoarea tactica de fuzionare: radacina arborelui cu mai putine varfuri
devine fiu al radacinii celuilalt arbore. Comprimarea drumului nu modifica numarul
de varfuri intr-un arbore, astfel incat este usor sa memoram aceasta
valoare in mod exact (in cazul folosirii regulii de ponderare, dupa comprimarea
drumului, nu se pastreaza inaltimea exacta a unui arbore).
Scrieti o procedura merge4 care urmeaza aceasta tactica si demonstrati un rezultat corespunzator Exercitiului 3.9.
3 .12 Gasiti un algoritm pentru a determina
daca un graf neorientat este conex. Folositi o structura de multimi disjuncte.
Indicatie: Presupunem ca graful este reprezentat printr-o lista de muchii. Consideram initial ca fiecare varf formeaza o submultime (in acest caz, o componenta conexa a grafului). Dupa fiecare citire a unei muchii {a, b} operam fuzionarea merge3(find3(a), find3(b)), obtinand astfel o noua componenta conexa. Procedeul se repeta, pana cand terminam de citit toate muchiile grafului. Graful este conex, daca si numai daca tabloul set devine constant. Analizati eficienta algoritmului.
In general, prin acest algoritm obtinem o partitionare a varfurilor grafului in submultimi doua cate doua disjuncte, fiecare submultime continand exact varfurile cate unei componente conexe a grafului.
3.13 Intr-o
structura de multimi disjuncte, un element x
este canonic, daca nu are tata. In procedurile find3 si merge3 observam
urmatoarele:
i) Daca x este un element canonic, atunci informatia din set[x] este folosita doar pentru a preciza ca x este canonic.
ii) Daca elementul x nu este canonic, atunci informatia din H[x] nu este folosita.
Tinand cont de i) si ii), modificati procedurile find3 si merge3 astfel incat, in locul tablourilor set si H, sa folositi un singur tablou de N elemente.
Indicatie: Utilizati in noul tablou si valori negative.
[*] In Exercitiul 3.2 sunt date si alte propozitii echivalente care caracterizeaza un arbore.
| Previous | Table of Contents | Next |